4.3. Преходни процеси в RC вериги

Преходни процеси във веригата фиг. 4.2 ще възникне, когато ключът K е настроен на позиция 1 (нулеви начални условия) или 2 (ненулеви начални условия).

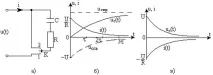
Ориз. 4.2. RC верига а) и преходни процеси в нея б) и в).

Преходен процес в RC-верига при нулеви начални условия. Разгледайте случая, когато на входа на веригата действа постоянно напрежение, т.е. u(t) \u003d U. В момента t \u003d 0 затваряме ключа K в позиция 1 и свързваме постоянно напрежение към веригата. Под действието на напрежение U, ток i ще тече във веригата, което създава спад на напрежението през резистора R и зарежда капацитета C. Въз основа на втория закон на Кирхоф можем да запишем

. (4.16)

Ще търсим решението на това уравнение под формата на сумата от общи и частни решения, които определят свободните и принудените компоненти:

. (4.17)

За да се определи свободната компонента, е необходимо да се намери решение на хомогенното диференциално уравнение, което се получава от (4.16) при U = 0 и има формата:

. (4.18)

Общото решение на уравнение (4.18) се дава от

, (4.19)

където А е константата на интегриране; p е коренът на характеристичното уравнение, получено от (4.18) RCp + 1 = 0, откъдето p = -1/RC = -1/τ, тогава (4.19) приема формата

, (4.20)

където τ = RC е времеконстантата на веригата.

В стабилно състояние (след зареждане на кондензатора) напрежението върху кондензатора ще бъде равно на напрежението, приложено към входа на веригата, т.е. принудителният компонент се определя от уравнението:

. (4.21)

Замествайки (4.20) и (4.21) в (4.17), имаме

. (4.22)

Като се има предвид, че в момента на превключване t = 0 и uC = 0 от (4.22) намираме константата на интегриране A = -U, тогава (4.20) ще приеме формата:

. (4,23)

Замествайки (4.21) и (4.23) в (4.17), получаваме израз, който определя как се променя напрежението на изхода на RC веригата, когато източник на постоянно напрежение е свързан към нейния вход

. (4,24)

Като се има предвид (4.24), намираме израз, който определя промяната на тока във веригата

. (4,25)

Графиките на напрежението (4.24) и тока (4.25), обясняващи преходния процес в RC веригата при зареждане на капацитета, са показани на фиг. 4.2б. От графиките се вижда, че в момента, в който източник на постоянно напрежение е свързан към RC веригата, токът във веригата достига максималната си стойност, а напрежението върху кондензатора е нула, т.е. капацитетът се държи като късо съединение на веригата. С увеличаване на времето токът намалява и напрежението върху капацитета нараства експоненциално. При t = 0 токът става нула и uC = U, т.е. капацитетът е еквивалентен на отворена верига за постоянен ток.

Нека разгледаме преходен процес в RC верига при нулеви начални условия, когато хармоничен ефект е свързан към входа на веригата. В този случай принудителният компонент ще изглежда така:

, (4.26)

(4,27)

Като вземем предвид (4.20) и (4.26), намираме

. (4,28)

Интеграционната константа A се определя въз основа на началните условия, че при t = 0 uC = 0, тогава

Замествайки A в (4.28), намираме израз, който определя промяната в UC при свързване към RC веригата на хармоничен ефект

. (4,29)

Токът във веригата се определя от израза

От израз (4.29) може да се види, че когато хармоничен ефект е свързан към RC верига с голяма времеконстанта τ в момента, когато φu = π - φ, във веригата могат да възникнат пренапрежения, достигащи стойности UCmax ≈ 2UmC. Ако към веригата е свързан хармоничен ефект, когато φu \u003d π / 2 - φ, тогава нямапреходен процес и незабавно настъпва стационарно състояние.

Преходен процес в RC-верига при ненулеви начални условия. Нека преведем ключа K във веригата на фиг. 4.2 в позиция 2. Това ще изключи веригата от входния източник и капацитетът ще бъде свързан към резистора R.

В момента на превключването капацитетът се зарежда до напрежение U и в него се съхранява енергия WC = CU2/2. След превключване капацитетът започва да се разрежда и енергията се изразходва на резистора R. Преходният процес, т.е. процесът на разреждане на капацитета се определя от уравнението

. (4,30)

Решението на уравнение (4.30) е израз (4.20)

. (4,31)

Интеграционната константа A се намира от началните условия, т.е. при t \u003d 0 uC \u003d U, след това от (4.31) определяме A \u003d U. Замествайки стойността A \u003d U в (4.31), намираме израз, който определя промяната на напрежението в RC веригата, когато капацитетът се разрежда през резистора

. (4,32)

Токът във веригата се променя в съответствие с израза

. (4,33)

Знакът (-) в уравнение (4.33) означава, че разрядният ток има противоположна посока на зарядния ток на капацитета.

Графиките на промените в uC и i са показани на фиг. 4.2, c.

От графиките на фиг. 4.2, c и изрази (4.32) и (4.33) се вижда, че в началото на разреждането на капацитета (t = 0), токът във веригата и напрежението върху капацитета имат максимални стойности uC = U, i = -U/R. С увеличаване на времето за разреждане, напрежението върху капацитета и тока във веригата се стремят към нула според експоненциалния закон, т.е. има преходен процес във веригата. Продължителността на преходния процес зависи от времеконстантата на веригата τ, която завършва след време t ≈ 3τ. Цялата енергия, съхранявана в кондензатора, се преобразува в топлина в резистора R по време на разреждането.