4.5. Методи за решаване на задачи от целочислено програмиране
Концепцията за целочислено програмиране
Ако в проблем с линейно програмиране е посочено като допълнително ограничение, че стойностите на променливите трябва да бъдат цели числа, тогава такъв проблем с линейно програмиране се нарича проблем с целочислено програмиране [19].
Ако целевата функция зависи само от две променливи, концепцията за целочислено програмиране може да бъде илюстрирана геометрично (Фигура 4.5.1). Допустимите решения на задачата не са целия диапазон от възможни стойности на тези променливи, а само отделни точки от равнината (1,2) с цели координати1 и2.
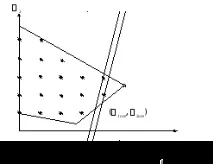
Ориз. 4.5.1. Областта на възможните решения за проблема с процесора
Точките на Фигура 4.5.1 маркират целочислените координати на диапазона от променливи1 и2, които по същество са целочислените стойности на оценките на алтернативите според критериите1 и2.
Когато решавате проблеми с целочислено програмиране, изглежда, че можете да използвате симплекса - метод за решаване на проблеми с LP, независимо от факта, че се въвежда допълнително ограничение върху целочислените стойности на променливите и след това да закръглите полученото решение до най-близката точка с цели координати. Въпреки това, полученото по този начин решение може да не е оптимално, тъй като дори и в случай на две променливи не е ясно до коя най-близка точка с целочислени координати трябва да се закръгли решението. На фиг. 4.5.1 има две такива точки: (4, 2) и (4, 3). Двете прави линии, показани на фиг. 4.5.1 съответстват на проекциите на две групи от точки от равнината на целевата функцияW(), разположени на еднакво разстояние вертикално от равнината (1,2) върху тази равнина. Правата линия, минаваща през точката (4, 2), съответства на по-голяма стойностW() отправа линия, успоредна на него, минаваща през точката (4, 3).
Има няколко метода за директно решаване на проблеми с целочислено програмиране. Най-разпространеният от тези методи е методът на Gomori (метод на отсечената равнина).
Метод на Гомори за решаване на проблеми
целочислено програмиране[19]
Този метод се основава на прилагането насимплексния метод, с помощта на който първоначално се намира оптималното решение на задачата на ЛП, без да се вземат предвид ограниченията върху целочислените променливи.
Ако стойностите на променливите, които дават оптималната стойност на целевата функция, са цяло число, тогава проблемът е решен и приложението на метода приключва.
В противен случай, т.е. когато стойността на поне една променлива се окаже нецяло число, трябва да се въведедопълнително линейно ограничение, което отрязва нецелочислена точка (1opt,2opt) от решението на задачата LP заедно с цялата област от възможни решения на проблема LP, която не съдържа inte ger решения. Добавеното изрязване (допълнително линейно ограничение) не отхвърля нито една от оригиналните валидни цели числа. Но всеки разрез трябва да премине през поне една валидна точка (валидна или не). Желаното ограничение (допълнително линейно ограничение) се изгражда на базата надробни компоненти на коефициентитена генериращияред на симплексна таблица, в колоната "Решение" на която има нецяло число. Такъв генериращ низ може да бъде иW()-низ, ако в оригиналната целева функция всички коефициенти преди променливите са цели числа (оттук следва, че за целочислени стойности на аргументите, стойността на целевата функция също е цяло число).
След това задачата LP с получената целфункция и нови ограничения (стари и едно допълнително) отново се решава чрез симплексния метод.
Ако новото решение все още не е цяло число, тогава итерацията се повтаря, т.е. въвежда се още едно допълнително ограничение и отново проблемът се решава по симплексния метод. И така нататък, докато се получи решение, в което стойностите на всички променливи са цели числа.