4D Polyhedron Wiki
В геометрията, 4-политопе политоп в 4-измерно пространство [1] [2] . Полиедърът е свързана затворена фигура, състояща се от многостенни елементи с по-ниско измерение - върхове, ръбове, лица (многоъгълници) и клетки [en] (3-измерни полиедри). Всяко лице принадлежи точно на две клетки.
2D аналогът на 4D политопите е многоъгълникът, а 3D аналогът е (3D) политопът.
Топологично 4-измерните полиедри са тясно свързани с еднакви пчелни пити [en] , като кубични пчелни пити [en] * подреждане на 3-измерно пространство. По подобен начин триизмерният куб е свързан с безкрайните двуизмерни квадратни пчелни пити. Изпъкнали 4D полиедри могат да бъдатизрязани и разгънатикато разгънати в 3D пространство.
Съдържание
Определение [код]
4-измерният полиедър е затворена 4-измерна фигура. Състои се от върхове (ъглови точки), ръбове, лица и клетки [en] . Клетката е 3D аналог на лице и е (3D) полиедър. Всяко (двуизмерно) лице трябва да свързва точно две клетки, точно както ръбовете на 3D полиедър свързват точно две лица. Подобно на други политопи, елементите на 4-политоп не могат да бъдат разделени на две или повече множества, които също са 4-политопи, т.е. той не е съставен.
Най-известният 4-измерен полиедър е тесерактът (хиперкуб), четириизмерен аналог на куба.
Визуализация [код]


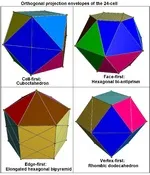
4-измерните полиедри не могат да бъдат представени в триизмерно пространство поради допълнителното измерение. За визуализация се използват редица техники.
ортогоналенпроекциите могат да се използват за показване на различни симетрии на 4-измерен полиедър. Проекциите могат да бъдат представени като двуизмерни графики или могат да бъдат представени като триизмерни тела като проективни обвивки [en] .
Точно както 3D форми могат да бъдат проектирани върху плосък лист, 4D форми могат да бъдат проектирани в 3D пространство или дори върху равнина. Често срещан тип проекция е диаграмата на Шлегел, която използва стереографска проекция на точки върху повърхността на 3-сфера в 3D пространство, свързани в 3D пространство чрез прави ръбове, лица и клетки.
Точно както изрязването на полиедър разкрива изрязана повърхност, изрязването на 4D полиедър създава "хиперповърхност" в 3D пространството. Последователността на такива резени може да се използва за разбиране на цялата фигура. Допълнителното измерение може да се приравни към времето, необходимо за анимиране на тези секции.
Развитието на 4D полиедър се състои от полиедрични клетки [en], свързани с лица и разположени в триизмерно пространство, точно както многоъгълните лица на разработка на триизмерен многостен са свързани с ръбове и всички са разположени в една и съща равнина.
Топологични характеристики [ код ]
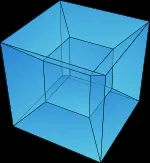
Топологията на всеки даден 4-политоп се определя от неговите числа на Бети и коефициенти на усукване [en] [3] .
Стойността на характеристиката на Ойлер, използвана за характеризиране на полиедри, не се обобщава правилно за по-високи измерения и е нула за всички 4-измерни полиедри, независимо от основната топология. Това несъответствие в характеристиката на Ойлер за надеждно разграничаване между различни топологии във високи размери води до появата на по-прецизни числа на Бети [3] .
ПодобенПо този начин концепцията за ориентираемост на полиедър е недостатъчна, за да характеризира усукването на повърхностите на тороидалните полиедри, което води до използването на коефициенти на усукване [3] .
Класификация [код]
Критерии [ код ]
4-измерните полиедри могат да бъдат класифицирани по свойства като "изпъкналост" и "симетрия" [3] .
- 4-политопът еизпъкнал, ако неговите граници (включително клетки, (3-измерни) лица и ръбове) не се пресичат (по принцип лицата на политопа могат да минават вътре в обвивката) и сегментите, свързващи всеки две точки от 4-политопа, се съдържат изцяло вътре в него. В противен случай политопът се счита занеизпъкнал. Самопресичащите се 4-измерни полиедри са известни също като звездовидни полиедри, по аналогия със звездообразните форми на неизпъкнали полиедри на Kepler-Poinsot.
- 4-многогранник еправилен, ако е транзитивен по отношение на своите флагове. Това означава, че всички негови клетки са конгруентни правилни полиедри, а също и всичките му фигури на върха са конгруентни на друг вид правилни полиедри.
- Изпъкнал 4-политоп еполуправилен, ако има група на симетрия, така че всички върхове са еквивалентни (върхът е транзитивен) и клетките са правилни политопи. Клетките могат да бъдат от два или повече типа, при условие че имат един и същ тип лице. Има само 3 такива фигури, открити от Торолд Госет[en] през 1900 г. - напълно съкратена петклетъчна[en] , напълно съкратена шестстотин[en] и изкривена двадесет и четири клетки[en] .
- 4-политоп ехомогенен[en], ако има група на симетрия, така че всички върхове да са еквивалентни и клеткитеса еднакви полиедри[en] . (Двумерните) лица на еднакъв 4-многоъгълник трябва да бъдат правилни многоъгълници.
- 4-политоп еизо-ребрен политоп[en][4], ако е върхово транзитивен и има ръбове с еднаква дължина. Тоест, допускат се нехомогенни клетки, например изпъкнали полиедри на Джонсън.
- Правилен 4-многогранник, който също е изпъкнал, се нарича правилен изпъкнал 4-многогранник[en] .
- 4-измерният полиедър епризматичен, ако е пряк продукт на два или повече полиедра с по-ниско измерение. Призматичен 4-измерен полиедър е хомогенен, ако неговите множители в прекия продукт са хомогенни. Хиперкубът е призматичен (произведението на два квадрата или куб и отсечка), но се разглежда отделно, защото има по-висока симетрия от симетриите, наследени от фактори.
- мозайка или пчелни пити в триизмерно пространствое разлагане на триизмерно евклидово пространство в повтаряща се решетка [en] от полиедрични клетки. Такива плочки или теселации са безкрайни и не са ограничени от "4D" обем, така че те са примери за безкрайни 4-полиедра.Хомогенно подреждане на триизмерно пространствое подреждане, в което върховете са конгруентни и свързани с кристалографска група, а клетките са равномерни полиедри[en].
Класове [код]
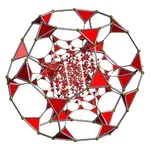
- Изпъкнали хомогенни 4-измерни полиедри(64, плюс две безкрайни семейства)
- 47-те непризматични изпъкнали равномерни 4-политопа включват:
- 6 правилни 4-измерни полиедра
×: Дуопризми (безкрайно семейство)

Други изпъкнали 4-измерни полиедри:

Безкрайни хомогенни 4-измерни полиедри в Евклидово 3-измерно пространство(хомогенни подреждания чрез изпъкнали хомогенни клетки)
Безкрайни хомогенни 4-политопи на хиперболично 3-измерно пространство?!(хомогенни плочки с изпъкнали хомогенни клетки)
- 41 уникални двойствени хомогенни 4-многополитопи
- 17 уникални двойни хомогенни полиедрични призми
- безкрайно семейство от двойни изпъкнали хомогенни дуопризми (с неправилни тетраедрични клетки)
- 27 уникални двойни хомогенни клетки, включително:
- Ромбични додекаедрични пчелни пити[en]
- Изоедрични тетраедрични пчелни пити[en]
- Weir-Phelan структура[en] на периодични запълващи пространството пчелни пити с неправилни клетки