Abstract Optics - Банка с резюмета, есета, доклади, курсови работи и дипломни работи
Работата е на Балтина Елена, 9 "А" клас
Министерство на общото и професионалното образование на Свердловска област
Управление и образование на Орджоникидзевски район.
Оптиката е дял от физиката, който се занимава с изучаването на природата на светлината, законите на нейното излъчване, разпространение и взаимодействие с материята. Реших да напиша проект на тема "Оптика", тъй като в момента оптиката е намерила своето приложение в много области на науката, технологиите и човешката дейност.
геометрична оптика
§1. Експериментални закони.
Оптиката изучава излъчването, разпространението и взаимодействието с материята на широк спектър от електромагнитни вълни - от милиметрови радиовълни до твърдо γ-лъчение. Хората се доближиха до концепцията за електромагнитната природа на светлината едва през 19 век. Първоначално в оптиката се изучава видимата светлина, излъчвана от светлинни източници – химични, биологични, физични. Физическите източници включват горещи тела и луминисцентни източници на студена светлина. Други тела отразяват светлината и затова са видими.
В оптиката се използват различни светлинни лъчи - събиращи се или разминаващи се. Достатъчно тесен светлинен лъч, слабо сближаващ се или отклоняващ се, се нарича светлинен лъч.
Устройството, с което се преобразуват лъчите, е оптична система. Източникът на лъчи (собствени или отразени) е обект. Лъчите, преминаващи от обекта към системата, са входящи. След трансформация в системата се получават изходящи лъчи.
За една оптична система се казва, че е идеална, ако всеки входящ лъч съответства на един изходящ. В този случай всички входящи лъчи, идващи от една точка, се пресичат (или се разминават, така че техните продължения да се пресичат), напускайки системата, в една точка. Тази точкапресичане - изображението на тази точка.
За да се построи изображение на точка в идеална система, е достатъчно да се построят всеки два лъча, излизащи от тази точка. Пресечната точка на изходящите лъчи, съответстващи на тези два падащи лъча, ще бъде желаното изображение на тази точка.
Лъчите, излизащи от оптичната система, могат да се събират или да се разминават. В първия случай те се пресичат в точката на реалното изображение. Във втория случай точката на пресичане на продълженията на изходящите лъчи ще бъде виртуално изображение.
Образът на обект в идеална система е съвкупност от изображения на неговите точки. Това е растерна графика.
Изучавайки света около нас, човечеството е натрупало голямо количество експериментална информация за светлината.
Отражението и праволинейността на разпространението на светлината са били известни преди около две хиляди години. В началото на XVII век. бяха формулирани законите на пречупването. Всичко това е предмет на геометричната оптика.
Законът за обратимостта на светлинните лъчи. Нека лъч A падне върху някаква идеална оптична система и от нея излезе съответният лъч B. Ако започнем нов падащ лъч към B, получаваме нов лъч, излизащ от системата, отиващ към A.
Законът за праволинейното разпространение на светлината. В хомогенна среда светлината се разпространява по права линия. Ние възприемаме източника на светлина или обекта, от който е паднала отразената светлина, върху продължението на лъчите, които попадат в окото. Този закон обяснява образуването на геометрична сянка, фотографиране с камера обскура (безобективна камера с малък отвор).
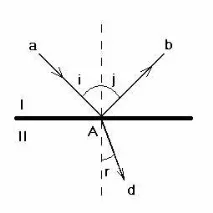
Закони на отражението. Границата на две среди е повърхността, разделяща две еднородни среди (I и II, фиг. 1). Светлинен лъч, отиващ до границата в среда I (която е първата именно защото от нея догранична падаща греда), се нарича инцидент (a). Лъчът, оставащ в среда I след взаимодействие с границата в точката на падане A, се отразява (c).
Ъгълът i между падащия лъч и перпендикуляра, възстановен към границата на две среди в точката на падане, е ъгълът на падане. Ъгълът j между отразения лъч и перпендикуляра на границата на две среди в точката на падане е ъгълът на отражение. Равнината, в която лежат падащият лъч и перпендикулярът към границата на две среди в точката на падане, е равнината на падане.
2. Ъгълът на падане е равен на ъгъла на отражение (променяйки произволно ъгъла на падане, получаваме същата промяна в ъгъла на отражение):
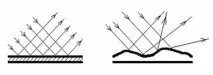
Има огледални и дифузни отражения. Отражението се нарича огледално отражение, при което паралелен сноп светлинни лъчи, падащ върху повърхността, остава успореден (фиг. 2). Отражението се нарича дифузно, при което падащият паралелен лъч се разсейва (фиг. 3).
Съответно се разграничават огледални (достатъчно гладки) и матови (разсейващи) повърхности. Това са относителни понятия. Една повърхност може да бъде огледална и матова за различни излъчвания. Дори при едно лъчение, матовата повърхност може да стане огледална, ако ъгълът на падане се увеличи.
Закони за пречупване. На границата на две среди, в допълнение към отражението, се наблюдава пречупване - явление, състоящо се в това, че лъчът частично преминава във втората среда, променяйки първоначалната си посока. Този лъч се нарича пречупен (d, фиг. 1). Ъгълът r между пречупения лъч и перпендикуляра на границата на две среди в точката на падане се нарича ъгъл на пречупване.
1. Падащ лъч, перпендикулярен на границата на две среди в точката на падане и пречупеният лъч лежат в една равнина (подобно на първия закон на отражението, смисълът на този закон е, че третата от изброените линии удря равнината,чиято позиция се определя от първите две. Това е равнината на падането).
2. Съотношението на синуса на ъгъла на падане към синуса на ъгъла на пречупване е постоянна стойност за дадена двойка медии (т.е. не се променя с произволна промяна на ъгъла на падане и съответното изменение на ъгъла на пречупване). Тази константа се нарича индекс на пречупване (n21) на втората среда спрямо първата:
n21=sin i / sin r. (2)
Коефициентът на пречупване на всяка среда спрямо вакуума се нарича абсолютен индекс на пречупване n.
Нека оставим лъч да пада на границата по d (фиг. 1), пречупеният лъч, съгласно закона за обратимостта, ще премине в средата I по посока a. Това означава (ако не промените обозначенията на ъглите),
sin r / sin i \u003d n12 \u003d 1 / n21. (3)
Коефициентите на пречупване на първата среда спрямо втората и на втората среда спрямо първата са реципрочни.
Ако ъгълът на падане е по-голям от ъгъла на пречупване, тогава се казва, че втората среда е оптически по-плътна от първата и обратно. Това определение е относително, ако втората среда е оптически по-плътна от първата, тогава първата среда е оптически по-малко плътна от втората. При преминаване в оптически по-плътна среда лъчът се отклонява от първоначалната посока към основата на перпендикуляра, синусът на ъгъла на падане е по-голям от синуса на ъгъла на пречупване, а показателят на пречупване е по-голям от единица. При преход към оптично по-малко плътна среда, напротив, индексът на пречупване е по-малък от единица.
§2. Плоско огледало.
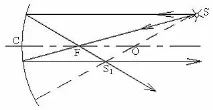
Нека разгледаме всеки два лъча, падащи от източник S в произволни точки A и B на плоско огледало (фиг. 4). Отразените лъчи, конструирани в съответствие с формула (1), се разминават, техните разширения ще се пресичат в точката S1, която ще бъде въображаем образ на източника S (ако продълженията и всички други отразенилъчи!).
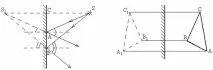
Триъгълниците SAB и S1AB имат обща страна AB и равни двойки ъгли A и B [ъглите, отбелязани с дъга в точка A, са равни по формулата (1) и като вертикални, ъглите, отбелязани с две дъги в точка B, са равни по подобен начин. Но всеки ъгъл A в нашите триъгълници е равен на прав плюс един от маркираните, което означава, че те се навиват един друг; всеки ъгъл B е равен на права линия минус маркираните, което означава, че те също са равни един на друг]. Такива триъгълници са равни, следователно техните подобни елементи са равни, по-специално височините, перпендикулярни на огледалото.
Следователно, за всеки триъгълник SAB, съответната височина е перпендикулярът на огледалото, равен на разстоянието SC, и всички лъчи ще бъдат отразени от огледалото, така че техните продължения ще преминат през точката S1, която ще бъде образът на точката S. Огледално-симетричната точка S1 (по отношение на равнината AB) е точката, лежаща на перпендикуляра на равнината, спусната от точката S на същото разстояние от нея: SC \u003 d S1C.
Нека изградим изображение на обекта (триъгълник ABC, фиг. 5) в плоско огледало. Вече не могат да се изграждат лъчи, знаем, че образът на всяка точка в огледалото ще бъде огледално-симетрична точка. Изображението A1B1C1 е въображаемо (продълженията на лъчите се пресичат, не можете да получите изображение на екрана, поставен зад огледалото), право, равно, но огледално симетрично (т.е. отражението на лявата страна на обекта е дясната страна на изображението и т.н.). За да се убедите в това, достатъчно е да си представите движението на автомобили, движещи се една срещу друга от дясната (за себе си!) страна на пътя. Погледнете се в огледалото и се уверете, че часовникът е на изображението ви от дясната ръка и т.н. Отпечатъкът на текста върху попивателната хартия е труден за четене - има букви "обратно". В огледалото изображението се обръща отново илесен за четене.
§3. сферични огледала.
От всички неравнинни огледала ще разгледаме само сферичните, чиято отразяваща повърхност е външната или вътрешната част на сферата. Имаме вдлъбнато огледало (фиг. 6). Средата C на огледалото се нарича полюс.
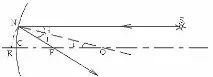
Всеки лъч, паднал върху огледалото през центъра на сферата (ъгълът на падане е нула), отразен, ще отиде в същата посока. Има само една точка O, която удовлетворява това условие. Нарича се оптичен център на огледалото. Всички прави, минаващи през оптичния център, са оптичните оси на огледалото. Една от оптичните оси минава през полюса C на огледалото, това е главната оптична ос. Останалите оптични оси са вторични.
Нека лъч, успореден на главната оптична ос, пада върху огледалото в точка N. NO е радиусът и следователно е перпендикулярен на сферата. Като построим ъгъла на отражение, равен на ъгъла на падане, получаваме отразения лъч NF. Ъглите на падане i и NOF са равни, тъй като вътрешните напречно лежат на успоредни прави и секуща. Следователно триъгълникът NOF е равнобедрен и ׀NF׀=׀FO׀.
Начертайте дъга NK с радиус FN. Пресечната точка на дъгата с главната оптична ос не съвпада с точка C, но е близо до нея. Отсечката ׀SK׀ е толкова по-малка, колкото SN е по-близо до главната оптична ос. Ограничаваме се до параксиални (параксиални) греди, така че можем да считаме сегмента ׀CK׀«׀CF׀ за пренебрежимо малък. За такива лъчи ׀CF׀=׀NF׀=׀FO׀, а точката F за всички параксиални лъчи лежи в средата на радиуса CO. Тази точка се нарича главен фокус на огледалото (разбира се, има фокуси по всички останали оптични оси - вторични). И така, основният фокус на вдлъбнато огледало е точката, в която след отражение се пресичат всички параксиални лъчи, падащи успоредно на главната оптична ос.
Подобни разсъжденияи конструкциите ще ни доведат до концепцията за въображаемия основен фокус на изпъкнало огледало (фиг. 7). Разстоянието от огледалото до главния фокус се нарича фокусно разстояние и се обозначава с F. Може да се докаже, че всички лъчи, падащи от една точка, след отражение от вдлъбнато огледало, преминават през една точка - изображението (това може да се докаже поне чрез конструкция; поради приближаването на условието за параксиалност, това, разбира се, не е съвсем точка, а малко петно, за изпъкнало огледало - това е точката на пресичане на продължението на всички отразени лъчи ). За да се построи такава точка, са достатъчни всеки два лъча. Лъч, падащ успоредно на главната оптична ос, след отражение ще премине през главния фокус (или продължението на отразения лъч ще премине през главния фокус - за изпъкнало огледало). Според закона за обратимостта лъчът, падащ през главния фокус, след отражение ще премине успоредно на главната оптична ос. И накрая, лъч, падащ през центъра на сферата, ще се отрази в същата посока.
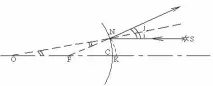
При конструиране на изображение точките във вдлъбнато огледало (фиг. 8) маркират точки O, F, C, след което се изграждат всеки два от трите изброени лъча. Всички други отразени лъчи също ще преминат през точката на пресичане на отразените лъчи S1 - това е реалният образ на точката S. Конструкцията на изображението в изпъкнало огледало е подобна.
Нека изградим изображение на обект AB във вдлъбнато огледало (фиг. 9). Изображение A1 се намира, както на фиг. 8. Изграждането на изображението на точка, разположена на главната оптична ос, се извършва по следния начин: изчертаваме произволен лъч VM и успоредно на него съответната странична ос OD; в средата на разстоянието OD има страничен фокус F1, през който ще премине отразеният от точката M лъч. Като втори лъч е удобно да изберете лъч, преминаващ по главната оптична ос. Точкапресичане на два отразени лъча - изображение B1.
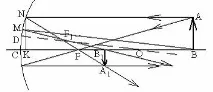
Нека означим разстоянието от огледалото до обекта d=׀CB׀; разстояние от огледалото до изображението f=СB1; фокусно разстояние F=׀CF׀≈׀KF׀. От подобието на триъгълници А1В1F и NKF следва равенството
аналогично, от подобието на триъгълници A1B1O и ABO
Следователно (f – F)/F=(2F – f)/(d – 2F).
2F2 - Ff=fd - Fd - 2Ff + 2F2
Разделяме това уравнение на произведението Ffd:
(4)
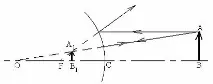
Получихме огледалната формула. Може да се приложи и към изпъкнало огледало. Подобна конструкция за изпъкнало огледало (фиг. 10) показва, че ако обектът е разположен пред огледалото (d > 0), тогава изображението е разположено от другата страна на огледалото (f Страници:12 3