Алгоритъм на Евклид
Когато казват „число за деление“, те имат предвид, че то се дели без остатък. Така че A се дели на B само ако остатъкът от тяхното деление е нула. Концепцията за най-голям общ делител (НОД) се основава на това свойство. НОД на две числа е най-големият от всички техни общи делители.
Алгоритъм на Евклид чрез изваждане.
Намирането на gcd на две цели числа е малко по-лесно с помощта на операцията за изваждане. За да направите това, трябва да изпълните следното условие: ако A=B, тогава НОД е намерен и е равен на едно от числата, в противен случай трябва да замените по-голямото от двете числа с разликата между него и по-малкото.
Блок-схема на алгоритъма на Евклид чрез изваждане:
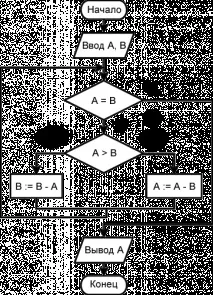
Работейки с тази блокова схема - съставяйки програмния код по нея, е доста целесъобразно в нея да се включи оператор за цикъл с вложен оператор за условно разклоняване, имащ две разклонения.
Програмен код на C++ (изваждане):
Програмен код на Pascal (изваждане):
Алгоритъм за деление на Евклид.
Вторият метод се различава от първия по това, че в основната част на програмата операцията за изваждане се заменя с операция за деление или по-скоро с вземане на остатъка от разделянето на голямо число на по-малко. Този метод е за предпочитане пред предишния, тъй като в повечето случаи е по-ефективен и отнема по-малко време. На конкретни примери ще демонстрираме работата на всеки тип изпълнение на алгоритъма.
Нека започнем с тази, която се основава на операцията за вземане на остатъка от делението. Имаме две числа: 112 и 32. Първото е по-голямо от второто - ще го заменим с остатъка от деленето на 112 на 32. Новата двойка числа включва 16 и 32. Второто е по-голямо, така че също ще го заменим с остатъка от деленето на 32 на 16, т.е. нула. В резултат на това получаваме GCD=16. Това изглежда така в таблица:
Сега нека компенсираме същите числатаблица за алгоритъма за изваждане.
Горният пример показа как в конкретен случай, като предпочете делението (вземане на остатъка от делението) пред изваждането, човек може да спечели в скоростта. Предимството на разделянето става по-ясно след следните съображения. Да предположим, че A е по-малко от B и тъй като gcd на две цели числа е по-малко или равно на най-малкото от тях, тогава и тук то е по-малко или равно на A; следователно ще бъде оптимално още при първата операция да замените B с число, по-малко или равно на A.
Освен това е известно, че в единия случай по-голямото число се заменя с разликата между него и по-малкото число, а в другия - с остатъка от делението. При деление на B на A (по-голямо на по-малко), остатъкът не може да надвишава числото в знаменателя (т.е. A), следователно вземането на остатъка от делението гарантира оптималния резултат. Но същото не може да се каже за операцията за изваждане, тъй като не е необходимо веднага след извършването на първото изваждане B да стане по-малко или равно на A. Например, нека A е 150 и B 1100. Така че, използвайки изваждане, ще получим B равно на 950 в първата стъпка, докато методът на делене ще даде 50.
Диаграма на алгоритъма за деление на Евклид:
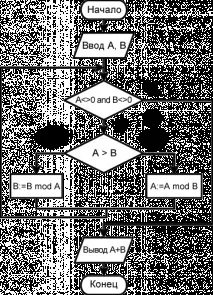
С изключение на условието за излизане от цикъл и операциите в изрази, тази блок-схема е подобна на предишната. Достатъчно е условието, при което тялото на цикъла да бъде изпълнено, докато и двете променливи имат стойности, различни от нула, тъй като когато условието престане да бъде вярно, от това ще следва, че една от текущите стойности е желаният най-голям общ делител. И тогава няма начин да се предотврати следващата итерация, в която ще бъде направен опит за деление на нула.