Алгоритми за засенчване на многоъгълници
Всяка ограничена област се дава чрез описание на нейната граница. Ако границата съдържа криволинейни участъци, тогава по време на визуализацията те предварително се апроксимират с прекъснати линии. Следователно можем да се ограничим до разглеждането на методите за рисуване на многоъгълни области.
Граничният многоъгълник на региона се определя от подреден списък от върховеPg= (P1, P2, . . , Pn), който описва затворена многоъгълна линия.За пълнотата на формалното описание на многоъгълен регион е важно също да се посочи правило, което определя коя страна на гранична линия са разположени най-близките вътрешни точки на региона.
Едно от най-простите и разбираеми правила за определяне на вътрешните точки на дадена област може да се формулира по следния начин: всяка точка от равнината е вътрешна точка на многоъгълник, ако лъч, изтеглен от нея във всяка посока, пресича границата на този многоъгълник нечетен брой пъти (фиг. 1.7). Броят на точките на пресичане на всяка права линия с границата ще бъде четен. Освен това, когато се движите по права линия, точките на влизане в полигона и излизане от него ще се редуват.
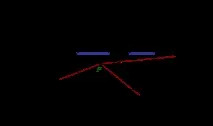
Горното е вярно и за хоризонтални растерни линии (Y= Const). Следователно многоъгълникът може да се запълва ред по ред, варирайки от ординататаYminна най-долния връх на многоъгълника до ординататаYmaxна най-горния му връх. Ако списъкът с точки на пресичане на страните на многоъгълника с низаYе сортиран по възходящи или низходящи координатиx, то всяка следваща двойка точки в списъка ще определя границите (xl, Y) и (xr, Y) на запълвания сегмент (фиг. 1.7).
Изчисляването на границиYminиYmaxзасенчване чрезYпозволява да се намали броят на разглежданите редове.Въпреки това, поради различни причини, например поради мащабиране, многоъгълникът може частично или напълно да излезе извън интервалаY, къдетоYemaxе максималната стойност на координататаyна изходната област. За да се избегнат неубедителни изчисления в тези случаи, намерените стойности трябва да бъдат коригирани, както следва:
(1,22)
(1,23)
При прилагането на метода трябва да се вземат предвид случаите, които изискват специална обработка. Първо, това са върховете на многоъгълника. Във всеки връх две съседни страни са спрегнати. Ако при рисуване се вземат предвид всички точки на пресичане на страни с линии, без да се изключва началото и края, тогава всеки връх ще съответства на две съвпадащи граници на сегмента, което в много случаи може да доведе до неправилно рисуване. Вторият специален случай на засенчване са хоризонталните страни (∆y =0) на граничния многоъгълник, тъй като те не пресичат растерните линии, а лежат върху тях.
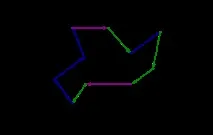
На фиг. Фигура 1.8 показва пример за граничен контур на многоъгълник, на който специални случаи са отбелязани с цифри: 1 - това са върхове, които трябва да се обработват като граница на един сегмент; 2 - върхове, които трябва да се разглеждат като две съвпадащи граници; 3 – гранични върхове на хоризонтални страни.
Ако за която и да е странаPiPi+1 увеличение сyизчислете като
, (1,24)
тогава случаи 1 и 2 са лесни за разграничаване един от друг чрез знака на нарастванията∆yна съседни страни, съседни на върховете. В случай 1 те са еднакви, а в случай 2 са противоположни.
За правилно обработване на специални случаи ще приемем следното правило: ако страната на многоъгълника е насочена нагоре (∆y >0), тогава ще изключим началния му връх от изчисляването на пресечните точки с редове и обратно, ако странатамногоъгълник е насочен надолу (∆y
(1,25)
Лесно се вижда, че освен страните, които не се пресичат с низаY, това условие също блокира обработката на хоризонталните страни, както и началните върхове за страните, насочени нагоре, и крайните върхове за страните, насочени надолу, т.е. осигурява правилното изчисляване на границите на сегментите в специални случаи.
Като се вземат предвид направените заключения, алгоритъмът за засенчване ще изглежда като този по-долу.
1. Последователно разглеждане на списъка с върхове (P1, P2, .. , Pn),намерете границите на сканиранеYminиYmax.
2. ИзчислетеYmin= max(Ymin, 0);Ymax= min(Ymax,Yеmax).
3. За всеки редYот [Ymin . . Ymax] изпълни p.p. 3.1. – 3.4.
3.1. Изчистване на списъкаXb.
3.2. За всичкиiот [1. . n] изпълнява т. 3.2.1. – 3.2.2.
3.2.1. Акоi = Y)) или ((yi >= Y) и (yk 0) са десните граници, а долните страни са (∆y0, и в списъкаXlв противен случай. Когато бъдат намерени всички точки на пресичане на страните на многоъгълника с низа, броят на елементите в списъцитеXlиXrтрябва да е същото.
Ако граничният многоъгълник е ориентиран така, че външната зона трябва да бъде боядисана (по посока на часовниковата стрелка), тогава всички линии, които нямат пресечни точки с многоъгълника, трябва да бъдат боядисани изцяло (фиг. 1.11). За останалите редове списъкътXlняма да съдържа лявата граница на първия сегмент за попълване, а списъкътXrняма да съдържа дясната граница на последния сегмент от реда. В тези случаи, за рисуване в рамките на изходната област, липсващата лява граница на първия сегмент трябва да се приеме католявата граница на изходната област и като липсващата дясна граница на последния сегмент от линията, дясната му граница.
Ориентацията (по или обратно на часовниковата стрелка) на граничния многоъгълник може да се определи аналитично. Това не изисква анализ на относителната позиция на всички върхове. Ориентацията на граничния многоъгълник е същата като ориентацията на неизродения триъгълник, дадена от най-високия или най-ниския връх на многоъгълника и двата му съседни върха. За категоричност намираме в списъкаPgнай-високия връхPjи два съседни на него върхаPj-1 иPj+1 (фиг. 1.11).

Известно е, че площта на триъгълник, дадена от координатите на върховете, в този случай върховетеPj-1,PjиPj+1, се определя по формулата
. (1,26)
Анализът показва, че стойността на площта, изчислена по тази формула, е положителна, ако заобикалянето на точкитеPj-1,Pj,Pj+1 съответства на движение обратно на часовниковата стрелка и отрицателно, ако заобикалянето на тези точки съответства на движение по посока на часовниковата стрелка. Ако се разглежда област без самопресичане, тогава ориентацията на цялата област съвпада с ориентацията на дадения триъгълник. Ако избраните точки лежат на една и съща права линия, тогаваS= 0. Очевидно, заS= 0, точкатаPjе в центъра на веригата от хоризонтални страни. В този случайjтрябва да се увеличи доS≠ 0.
По-долу е даден алгоритъм за засенчване на ориентирани полигони, изграден на базата на горното.
1. Преглеждайки последователно списъка с върхове (P1,P2 , . . ,Pn), намерете индексаjна най-високия връх, както и границите на сканиранеYminиYmax.
2. ИзчислетеYmin= max(Ymin, 0);Ymax=min(Ymax, Yеmax).
4. АкоS= Y)) или ((yi >= Y) и (yk 0, тогава напишетеxнаXr, в противен случай напишетеxнаXl.
5.3. АкоSxr, тогава засенчването не трябва да се прави.