A_Magnet Програма-калкулатор на индукцията на магнитното поле на пръстеновиден (цилиндричен) магнит

A_Magnet: Калкулатор за индукция на магнитно поле за пръстеновиден (цилиндричен) магнит, използващ метода на еквивалентен соленоид

Теория

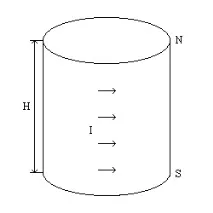
Ориз. 1. Представяне на цилиндричен постоянен магнит чрез еквивалентен соленоид.

Постоянният магнит с аксиална посока на намагнитване, по-специално цилиндричен, може да се разглежда като еднослоен соленоид с безкрайно тънка намотка, геометрично съответстваща на страничната повърхност на магнита, през която протича магнетизиращият ток I (виж фиг. 1). Условието за еквивалентност на магнит и соленоид е равенството на техните магнитни моменти. Магнитният момент на магнит ( P) може да се намери по формулата:

P = M V = M S H, където M е намагнитването на магнита, V е неговият обем, S е площта на напречното сечение, H е височината.

Магнитен момент на еквивалентния соленоид:

P = j H S, където j = I/H е линейната плътност на намагнитващия ток.

За материали с правоъгълна хистерезисна верига (бариев ферит, стронциев ферит, неодим-желязо-бор, самарий-кобалт и др.):

Br/ m 0, където Br е остатъчната индукция, m 0 = 4 p ∙ 10 -7 H/m е магнитната константа. По този начин линейната плътност на намагнитващия ток може да се изрази с приблизителната формула:

Пръстеновиден постоянен магнит с аксиална посока на намагнитване може да бъде представен като два еднослойни цилиндрични соленоида с безкрайно тънки намотки, вложени една в друга. Соленоидът с диаметър D2 и височина H съответства на външната странична повърхност на магнита, а соленоидът с диаметър D1 и височина H съответства на вътрешната повърхност на отвора. Магнитните токове в соленоидите са еднакви по големина и противоположни по посока.

Изчислете величината и посоката на вектора на магнитната индукцияBв произволна точкамагнитното поле, създадено във вакуум (или въздух) от еднослоен соленоид с известна линейна плътност на тока, може да се получи с помощта на закона на Biot-Savart-Laplace [2].

Програма за пръстеновидни магнити (A_Magnet)

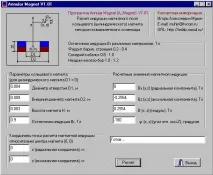
Ориз. 2. Външен вид на прозореца на програмата A_Magnet (версия 1.01).

Входни данни: D1 - диаметър на отвора на магнита, m D2 - външен диаметър на магнита, m H - височина на магнита, m Br - остатъчна индукция на материала на магнита, T x - радиус на точката (спрямо точка (0, 0) - център на магнита), където се изисква да се изчислят компонентите на магнитната индукция, m z - височина на точката (спрямо точка (0, 0) - магнитен център), където се изисква да се изчислят компонентите на магнитната индукция, m

Изходни данни: Bx (x, z) - радиална компонента на магнитната индукция в точка с координати (x, z) (спрямо точка (0, 0) - център на магнита), Тl Bz (x, z) - аксиална компонента на магнитна индукция в точка с координати (x, z) (спрямо точка (0, 0) - център на магнита), Тl B - модул на магнитна индукция в точката с координати (x, z) (спрямо точката (0, 0) - центърът на магнита), Тl f - ъгълът между вектора на магнитната индукция в точката с координати (x, z) и оста Z, градуси

Програмата A_Magnet ви позволява да изчислите стойността на магнитната индукция (B, Bx, Bz) в дадена точка от пространството (x, z) според зададените геометрични размери (D1, D2, H) на магнита и остатъчната индукция (Br) на материала, от който е направен магнитът. Изчисленията се правят в системата SI. Резултатите се показват на екрана на монитора.

Използвайки принципа на суперпозицията [2], могат да се изчислят магнитните полета на системи от пръстеновидни (цилиндрични) постоянни магнити.

Демо версия на A_Magnet:

Демо версияПрограмата ви позволява да изчислите индукцията на магнитното поле по оста на магнита (x = 0). Точността на изчислението е малко по-ниска, отколкото в основната версия. Програмата може да работи с операционни системи (ОС) Windows 3.1, Windows 95, 98, XP и Vista (други операционни системи от семейството на Windows не са тествани).

Файлът A_Magnet101d.rar трябва да бъде разопакован в предварително създадена папка. Опаковането беше направено с помощта на WinRar 2.80. Резултат от разопаковане: A_Magnet101d.exe - изпълним файл на програмата. След стартиране на програмата можете да въведете входните данни и да извършите изчислението, като натиснете съответния бутон. Входните данни (D1 - диаметър на отвора, D2 - външен диаметър на магнита, H - височина на магнита, x - радиална координата (x = 0), z - аксиална координата) трябва да бъдат въведени в метри (разгледайте формата на десетичния разделител, зададен в OS - точка или запетая, например 0,005 или 0,005; трябва да използвате разделителя, който е зададен в OS, в противен случай ще се появи съобщение за грешка). Остатъчната индукция Br се въвежда в тесла. Можете да проверите правилността на изчисленията на фиг. 2.

Копираните файлове могат да бъдат проверени за липса на вирусен код онлайн [5].

Експериментална проверка на програмата

Като един от примерите за експериментална проверка на програмата A_Magnet на фиг. Фигура 3 показва резултатите от изчисляването и измерването [6] на аксиалната компонента на магнитната индукция по оста на постоянен цилиндричен магнит. Размери на магнита: диаметър 14,5 mm (D2 = 0,0145 m), височина 20 mm (H = 0,02 m). Състав: неодим-желязо-бор, остатъчна индукция

1.1 T (Br = 1.1 T).

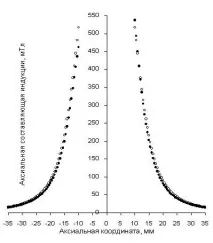
Ориз. Фиг. 2. Зависимост на аксиалната компонента на магнитната индукция от аксиалната координата: светли кръгове - изчислени стойности, тъмни кръгове - измеренистойности.

Известно несъответствие между измерените и изчислените стойности се обяснява с нееднородността на плътността на постоянния магнит, която възниква поради особеностите на технологията на производство.

Връзки:

Вигодски М. Я. Наръчник по висша математика. - М .: Издателство "Наука", гл. изд. физ.-мат. лит., 1977. - 872 с.; аз ще.
Закони и уравнения на магнитното поле
Корн Г., Корн Т. Наръчник по математика за учени и инженери. - М .: Издателство "Наука", гл. изд. физ.-мат. лит., 1968 г. - 720 стр.; аз ще.
Постоянни магнити: наръчник / Altman A. B., Gerberg A. N., Gladyshev P. A. и др.; Изд. Ю. М. Пятина. - 2-ро изд., преработено. и допълнителни - М.: Енергия, 1980. - 488 с., ил.
Проверка на потребителските файлове за вирусен код онлайн
Сканиране на магнитни полета (магнитно сканиране)
Яворски Б. М., Детлаф А. А. Наръчник по физика / За инженери и студенти. - 7-мо издание, Рев. - М .: Издателство "Наука", гл. изд. физ.-мат лит., 1978. - 944 с.; аз ще.

Магнитна индукция - вектор, числено равен на границата на съотношението на силата, действаща от магнитното поле върху проводниковия елемент с електрически ток, към произведението на тока и дължината на проводниковия елемент, ако дължината на този елемент клони към нула и елементът е така разположен в полето, че тази граница има най-голяма стойност и е насочен перпендикулярно на посоката на проводниковия елемент и на посоката на силата, действаща върху този елемент от магнитното поле, и от крайното му въртене по най-късото разстояние от посоката на силата до посоката на тока в елемента на проводника трябва да се види обратно на часовниковата стрелка.
Магнитно поле - вариацияелектромагнитно поле, създадено от движещи се електрически заряди или токове и упражняващо сила върху движещи се електрически заряди или токове.
Метод на еквивалентен соленоид - метод за изчисляване, базиран на представянето на постоянен магнит с аксиална посока на намагнитване под формата на еднослоен соленоид a с безкрайно тънка намотка, геометрично съответстваща на страничната повърхност на магнита, през която протича намагнитващ ток с такава величина, че магнитните моменти на соленоида и магнита са равни.
Намагнитване – магнитен момент на единица обем.
Операционна система (англ. операционна система) - основен набор от програми, които осигуряват работата на компютъра и взаимодействието му с потребителя.
Остатъчна индукция - стойността на магнитната индукция, която остава в пробата, след като силата на външното поле се намали до нула.
Постоянен магнит - обект, който създава магнитно поле поради собствените си вътрешни елементарни електрически токове, протичащи без използването на външен източник на енергия в материала, съставляващ обекта.
Цилиндричен соленоид- соленоид под формата на цилиндър с централен цилиндричен отвор (ако има такъв).