Аналитичен метод за кинематични изследвания, Лекции и примери за решаване на задачи по механика
С този метод връзките на механизма, неговите характерни размери и движенията на връзките се представят под формата на вектори. В резултат на това се образуват векторни полигони, на базата на които се съставят векторни уравнения.
Като се имат предвид тези векторни уравнения в проекции върху осите на произволно избрана координатна система, се получават системи от алгебрични уравнения, при решаването на които се извеждат уравнения за определяне на преместванията (линейни или ъглови) на изследваните връзки.
Параметърът е обобщената координата на началната връзка (обикновено ъгълът на въртене на входната манивела).
Чрез задаване на различни стойности на обобщената координата, получените уравнения определят позициите на изследваните връзки в различни позиции на механизма. Чрез двойно диференциране на уравненията на преместванията се получават уравнения за определяне на скоростите (линейни или ъглови) и ускоренията (линейни или ъглови) на изследваните връзки.
Въпреки това, както показва практиката, уравненията на скоростите и ускоренията, дори и за прости механизми, се оказват много тромави, с голяма вероятност да се получат грешки при многостепенна диференциация.
Освен това този подход изисква отделно програмиране за всеки механизъм при използване на компютър. Следователно (както беше показано по-горе) е удобно да се използва аналитичният метод в комбинация с графичния метод като алгоритъм за машинно решаване на проблема. Този подход прави решението на проблема много рационално.
Характеристика на групите на Асур от клас II от 1-ви и 2-ри тип е, че от геометрична гледна точка те имат две решения. Следователно прилагането на общия принцип за съставяне на аналитични уравнения, описан по-горе, води до решаването на сложни квадратни уравнения, които имат два корена.
Възниква нова задача за идентифициране на корена, който съответства на дадения механизъм. За да опростите решението на проблема, трябва да използвате следните препоръки:
- в групата от 1-ви тип, когато се съставя векторен полигон, е необходимо да се „премести“ от една крайна панта към друга, а не по връзките на групата;
- в групата от 2-ри тип, когато съставяте сумата от проекциите, е необходимо да начертаете спомагателна ос, перпендикулярна на водача, по който се движи плъзгачът, и да разгледате конструирания векторен многоъгълник в проекция върху тази ос.
Механизмът, показан на фигура 11, съдържа и двата случая. При формирането на векторен многоъгълник за първата част на този механизъм, който включва групата Assur от втория клас от първия тип, се изчертава вектор AC, свързващ крайните панти A и C на тази група (Фигура 11b).
В резултат на това се определят ъгълът γ и размерът AC, след което стават известни и трите страни в триъгълника ABC. Използвайки закона за косинусите, можете да определите всеки от ъглите на този триъгълник. В този случай се определя ъгълът α (Фигура 11c), защото за по-нататъшно решаване на проблема е необходимо да се знае ъгълът φ2.
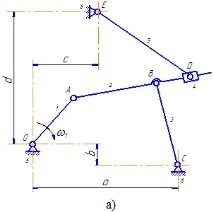
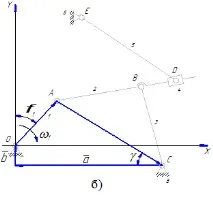

Векторен многоъгълник, включващ група от втори клас от втори тип, се разглежда в проекцията върху оста Y1, начертана перпендикулярно на водача ABD (Фигура 11c). Полученото алгебрично уравнение ни позволява да определим ъгъла β и след това желания ъгъл φ5.
По-конкретно, аналитичната дефиниция на ъгловото изместване на изходната връзка 5, показана на фигура 11 на механизма (като се вземат предвид горните препоръки), ще има следната форма:

Съгласно тези уравнения, с помощта на компютър, ъгловото преместване на изходната връзка φ5 в rad, ъгловата скорост ω5 вrad/s, ъглово ускорение ε5 в rad/s 2 за „n” позиции на предавка.