Атрактивни фиксирани точки
Бифуркация на Neimark-Sacker. Това е раздвоението на раждането
инвариантна крива. Провежда се при преминаване на горната граница
триъгълник на стабилност. Условие за намиране на тази бифуркация
има 1 J = . Тогава, в съответствие с формули (29), получаваме това
бифуркацията на Neumerk-Sacker се появява при −=μ a . По този начин,
условието за бифуркация на Neimark-Sacker не зависи от параметъра
Допирателна на бифуркации. Това раздвоение се получава, когато поне
един от множителите с фиксирана точка става плюс
мерна единица. Съответно се извършва при излизане от триъгълника
стабилност през дясната му граница. Условието за намиране на това
бифуркацията има формата
Замествайки в това уравнение изразите за следата и Якобиан (29), получаваме,
че допирателната бифуркация се извършва при 0 a = . Това е напълно
съответства на бифуркацията на седловия възел в прототипа на осцилатора.
В теорията на динамичните системиседловидна възлова бифуркацияе локална бифуркация, при която двойки сингулярни точки (стабилни и нестабилни) се сливат в полустабилна сингулярна точка (седловиден възел), която след това изчезва. Единствената бифуркация, която се среща в типичните еднопараметрични семейства от векторни полета на линията по неотстраним начин (тоест, е типична бифуркация на кодименсия 1).
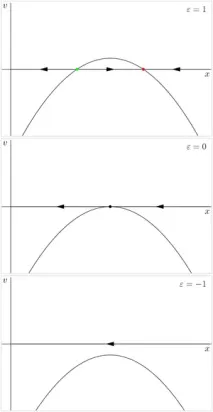
Да разгледаме векторно поле от права линия, която има особена точка. Ако сингулярната точка е неизродена (производната на векторното поле в нея е различна от 0), съгласно теоремата за неявната функция, тя се запазва при малки смущения и не възниква бифуркация. И така, най-простият случай, интересен от гледна точка на теорията на бифуркацията: първата производна е равна на нула. Обикновено втората производна е различна от нула.Разширявайки векторното поле в Тейлър е малко вероятно и променяйки координатната система, ако е необходимо, можем да приемем, че коефициентът е равен на -1. В този случай векторното поле има формата:
Тъй като сингулярната точка е изродена, векторното поле (1) не е структурно стабилно: произволно малко смущение може да разруши сингулярната точка или да я „разцепи“ на две. Оказва се, че всяко неизродено малко смущение на това векторно поле в околност на сингулярната точка 0 е (топологично) еквивалентно на еднопараметричното семейство
С други думи, това семейство ще бъде версална деформация за уравнение (1). Семейство (2) е нормалната форма на бифуркация на седловиден възел.
Помислете за семейството (2). Възможни са три случая:
Когато векторното поле има две особени точки:. Един от тях () е стабилен, другият () е нестабилен.
За , векторното поле има уникална полустабилна нехиперболична особена точка 0.
За , векторното поле няма особени точки.
По този начин бифуркацията на седло-възел може да се опише като процес на раждане на полустабилна сингулярна точка и нейното последващо разпадане в стабилна и нестабилна, или обратното, като процес на сливане на стабилна и нестабилна сингулярна точка в полустабилна с последващото й изчезване.
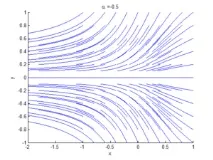
Бифуркация на седловина в равнината: >
Ако разгледаме двумерно фазово пространство и добавим уравнението към уравнение (2), при, сингулярната точка ще бъде стабилен възел, а сингулярната точка ще бъде седло. Сливайки се в, те образуват особена точка с една нулева и една ненулева собствена стойност, тоест седловиден възел. Това обяснява името на бифуркацията.
фиксирана точкана картографирането е точка, която картографирането преобразува в нея, с други думи, решението на уравнението.
напр.картографирането има фиксирани точки и , защото и .
Не всяко картографиране има фиксирани точки - да речем, картографирането на реална линия в себе си няма фиксирани точки.
Точките се връщат към себе си след определен брой итерации, тоест решаване на уравнението
се наричат периодични(по-специално, фиксираните точки са периодични точки от период 1).
Атрактивни фиксирани точки
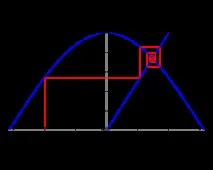
Намиране на решение на уравнението x=cos x
Фиксирана точка x=f(x) на картографирането f епривлекателна, ако итерациите на всяка начална точка y, достатъчно близо до x, клонят към x:
(В този случай обикновено се изисква итерациите на y да не напускат някаква по-голяма околност на точката x - т.е. точката x да бъде асимптотично стабилна.)
По-специално, достатъчно условие за привличане на точка е условието за производната: f'(x) 0 като последователности от повторения на картографирането
Стабилност на фиксирани точки на едномерно картографиране
Разгледайте процедурата за определяне на стабилността на фиксираните точки на картографирането (14.2). Ако стойността е в близост до фиксираната точка, тогава равенството е вярно:
където е малка стойност. Ако точката е стабилна, тогава с увеличаване на поредния номерnстойността трябва да намалява. Записваме връзка (14.2), като вземем предвид (14.5) и разширяваме дясната страна в серия на Тейлър:
Последното приблизително равенство е изпълнено толкова по-точно, колкото по-малък е . Като вземем предвид (14.3), получаваме:
Следователно, за да е в сила неравенството:
Това еусловието за стабилностна фиксираните точки на картографирането (14.2). Нека определим за какви стойности на параметъра фиксираните точки (14.4) ще бъдат стабилни. Производна на функцияf(x) на преобразуване (14.2) е равно на:
За фиксирана точка имаме:
Следователно точката е наистина стабилна при
Следователно точката ще бъде стабилна за стойностите на параметрите
Когато > 3, фиксираната точка губи своята стабилност.
Реалният процес, който се изследва, обикновено протича при определени външни условия, които в общия случай могат да се характеризират с определени стойности на параметрите на системата. Тези параметри също са включени в съответната система от диференциални уравнения. Така математическият модел приема формата:
където е векторът на системните параметри.Определение. Качествена промяна във фазовия портрет, която настъпва при промяна на системния параметър, се наричабифуркация на фазовия портрет. Стойността на системния параметър=0, при която възниква бифуркацията, се наричабифуркационна стойност на параметъра(илибифуркационна точка). Например, имаме уравнение: