Бройни системи, преводи на числа
ОТДЕЛЕНИЕТО ПО КОМПЮТЪРНА ТЕХНОЛОГИЯ.
Курсова работа по компютърни науки
Бройни системи, преводи на числа.
Изпълнил: студентът Иванов Д. Г.
Проверен от: Горохов А.Г.
Глава 1. История на развитието на бройните системи……………………………..2
1.1 Произходът на бройните системи…………………………………………………2
1.2 Образуване на десетичната бройна система……………………………. 4
Глава 2. Бройни системи…………….…………………………………..5
2.1 Позиционни и непозиционни бройни системи………………………5
2.2 Двоична (двоична) бройна система……………………………………….6
2.3. Осмична бройна система……………………………………………..6
2.4. Десетична бройна система…………………………………………. 6
2.5. Шестнадесетична бройна система……………………………………7
Глава 3. Представяне на числа в компютър…………………………………..8
3.1 Представяне на числа с фиксирана и плаваща запетая.………. …8
3.2 Числа с фиксирана точка…………………………………………….8
3.3 Числа с плаваща запетая……………………………………………………………9
3.3 Директни, обратни и допълнителни кодове. Променен код...10
Глава 4. Превод на числа…………………………………………………. 13
4.1 Представяне на двоични числа и преобразуването им в десетични…………….13
4.2 Преобразуване на десетични числа в двоични…………………………..13
6. Външен дизайн на програмата………………………………………15
7. Математически модел………………………………………………. 16
8. Кодиране и отстраняване на грешки в програмата…………………………………. …17
Глава 1. История на развитието на бройните системи.
1.1 Произход на бройните системи.
В ранните етапи от развитието на обществото хората почти не знаеха как да броят. Те разграничават един от друг комплекти от два и три обекта; всяка колекция,съдържащи по-голям брой предмети, се обединява в понятието „много“. Това все още не беше акаунт, а само негов зародиш.
Впоследствие се развива способността за разграничаване на малките агрегати един от друг; се появиха думи за понятията "четири", "пет", "шест", "седем". Последната дума дълго време означаваше и неопределено голям брой.
С усложняването на икономическата дейност на хората беше необходимо да се поддържа резултат в по-широк диапазон. За да направи това, човек използва предметите около себе си като инструменти за броене: прави прорези на пръчки и дървета, завързва възли на въжета, поставя камъчета на купчини и т.н. Това е удобно, тъй като броят на знаците веднага се определя визуално и се сравнява с броя на обектите, които тези знаци представляват. Всички отидохме в първи клас и броихме там на пръчки за броене - това е ехо от онази далечна епоха. Между другото, различни усъвършенствани инструменти произхождат от броенето с камъчета, като българско сметало, китайско сметало („лебедов тиган”), древноегипетско сметало (дъска, разделена на ивици, където са поставени жетони). Подобни инструменти съществуват сред много народи. Освен това на латински понятието "сметка" се изразява с думата "calculatio" (оттук и нашата дума "изчисление"); и идва от думата "calculus", което означава "камъче".
Особено важна роля играе естественият инструмент на човека - пръстите му. Този инструмент не можеше да съхранява резултата от преброяването дълго време, но винаги беше „под ръка“ и се отличаваше с голяма мобилност. Езикът на първобитния човек е бил беден; жестовете компенсираха липсата на думи, а числата, за които все още нямаше имена, бяха „показани“ на пръстите.
Ето защо е съвсем естествено, че нововъзникващите имена на "големи" числа честоса построени на базата на числото 10 - по броя на пръстите на ръцете; някои народи също са имали имена на числа, базирани на числото 5 - според броя на пръстите на едната ръка или на базата на числото 20 - според броя на пръстите на ръцете и краката.
Първоначално разширяването на запаса от числа беше бавно. Първоначално хората овладяха резултата в рамките на няколко десетки и едва по-късно стигнаха до сто. За много народи числото 40 отдавна е граница на броене и име на неопределено голямо число. на български думата "стоножка" има значението на "стоножка"; изразът "четиридесет и четиридесет" означаваше в старите времена число, което надминаваше всяко въображение.
На следващата стъпка броенето достига нова граница: десет десетици и се създава име за числото 100. В същото време думата "сто" придобива значението на неопределено голямо число. След това последователно числата хиляда, десет хиляди (в старите времена това число се наричаше „тъмнина“), един милион придобиват същото значение.
На настоящия етап границите на сметката се определят от термина "безкрайност", който не означава някакво конкретно число.
| Означаване на числата в различни бройни системи |
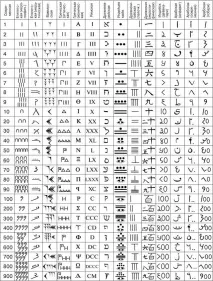
1.2 Формиране на десетичната бройна система.
В съвременния български език, както и в езиците на други народи, названията на всички числа до милион се състоят от 37 думи, обозначаващи числата 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1000 (например осемстотин и петнадесет хиляди триста деветдесет и четири). От своя страна, имената на тези 37 числа, като правило, се формират от имената на числата от първите десет (1, 2, 3, 4, 5, 6, 7, 8, 9) и числата 10, 100, 1000 (например 18 \u003d осем по десет, 30 \u003dтридесет и т.н.). Основата на това словообразуване е числото десет и затова нашата система от имена се нарича десетична бройна система.
В различните езици има различни изключения от това правило, които се обясняват с историческите особености на развитието на сметката. в българския език единственото изключение е името "четиридесет". Това изключение може да се свърже с факта, че числото 40 някога е играло специална роля, което означава неопределено голямо число.
В тюркските езици (узбекски, казахски, татарски, башкирски, турски и др.) Имената на числата 20, 30, 40, 50 са изключение, докато имената на числата 60, 70, 80, 90 се образуват от имената за 6, 7, 8, 9. Във френския недесетичните имена на числата 20 и 80 са запазени и 80 се нарича vingt , т.е. "четири и двадесет". Тук имаме остатъка от древното вигезимално изчисление (според броя на пръстите на ръцете и краката). На латински името на числото 20 също не е десетично (viginti). Имената на числата 18 и 19 се образуват от името 20 чрез изваждане: 20–2 и 20–1 (duodeviginti,undeviginti, т.е. „две от двадесет”, „едно от двадесет”).
Глава 2. Бройни системи.
2.1 Позиционни и непозиционни бройни системи.
Числовата системае система от техники и правила, които позволяват установяване на едно-към-едно съответствие между всяко число и неговото представяне като набор от краен брой знаци. Наборът от символи, използвани за това представяне, се наричацифри.
Бройните системи се делят на два класа - позиционни и непозиционни.
В непозиционните системи всяко число се определя като някаква функция на числовите стойности на набор от цифри,представляващи това число. Най-простата, но абсолютно неудобна бройна система. Базира се на една цифра - единица (стик). Позволява ви да пишете само естествени числа. За да представите число в тази бройна система, трябва да запишете толкова пръчици, колкото е самото число. Използван е от нецивилизовани племена, чиито нужди от броене по правило не надхвърлят първите десет. Чисто формално единичната бройна система може да се класифицира като основна (с основа 1). Но за разлика от останалите основни системи с числа, тя може да се счита за позиционна само с много силно разтягане и изобщо не е универсална (нула, дроби и отрицателни числа не могат да бъдат представени в нея). Римска цифрова система. С помощта на седем цифри - I=1 , V=5 , X=10 , L=50 , C=100 , D=500 , M=1000 - можете много успешно и доста изразително да представяте естествени числа от диапазона до няколко хиляди.
Исторически първите бройни системи са били именно непозиционни системи. Един от основните недостатъци е трудността при писане на големи числа. Записването на големи числа в такива системи е или много тромаво, или азбуката на системата е изключително голяма.
В компютърната техника непозиционните системи не се използват, но продължават да се използват в ограничена степен за обозначаване на поредни номера (часове, векове, номера на конгреси или конференции и др.).
Позиционна бройна система- бройна система, в която теглото на цифрата се променя с позицията на цифрата в числото, но се определя изцяло от изписването на цифрата и мястото, което заема. По-специално, това означава, че теглото на една цифра не зависи от стойностите на околните цифри. Такава бройна система се основава на факта, че определен брой n единици (основата на бройната система) се комбиниратв една единица от втора категория, n единици от втора категория се комбинират в една единица от трета категория и т.н. Основата на бройните системи може да бъде всяко число, по-голямо от едно. Сред такива системи е съвременната десетична бройна система (база n=10). В него числата 0,1, ..., 9 се използват за обозначаване на първите десет числа.