Четири прекрасни точки на триъгълника

Забележителните точки на триъгълникса точки, чието местоположение се определя еднозначно от триъгълника и не зависи от реда, в който са взети страните и върховете на триъгълника.

Свойства на точка, лежаща върху ъглополовящата на незавъртян ъгъл:

Теорема.Всяка точка от ъглополовящата на неразширен ъгъл е на еднакво разстояние от страните му.

Обратна теорема.Всяка точка, разположена вътре в ъгъл и на еднакво разстояние от страните на ъгъла, лежи върху неговата ъглополовяща.

Теорема.Симетралата на неразширен ъгъл е геометричното място на точките, еднакво отдалечени от страните на дадения ъгъл.

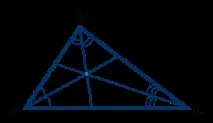
Симетралите на триъгълник се пресичат в една точка.

Перпендикулярната ъглополовяща на отсечкае права, перпендикулярна на тази отсечка и минаваща през средата му.

Свойства на точка, лежаща върху ъглополовящата на отсечка:

Теорема.Всяка точка от ъглополовящата към отсечка е на еднакво разстояние от краищата на тази отсечка.

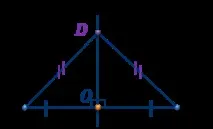
Обратна теорема.Всяка точка, еднакво отдалечена от краищата на отсечка, лежи на ъглополовящата към нея.

Теорема.Перпендикулярната ъглополовяща към отсечка е геометричното място на точките, еднакво отдалечени от краищата му.

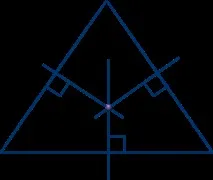
Перпендикулярните ъглополовящи на страните на триъгълник се пресичат в една точка.

Медианите на триъгълник се пресичат в една точка.

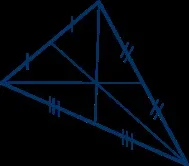
Височините на триъгълник (или техните продължения) се пресичат в една точка.

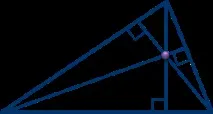
Вписани и описани окръжности

Ако всички страни на многоъгълник докосват кръг, тогава се казва, че кръгът е вписан в многоъгълника, а многоъгълникът се казва, че е описан около този кръг.

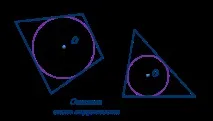
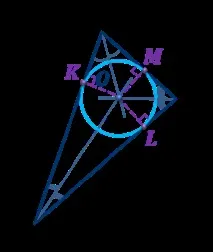
Теорема.Всеки триъгълник може да бъде вписанкръг.

Забележки.

1. Самоединкръг може да бъде вписан в триъгълник.

2. За разлика от триъгълника, не всекичетириъгълник може да бъде вписан в окръжност.

Ако кръг може да бъде вписан в четириъгълник, то неговите страни имат следното забележителносвойство:

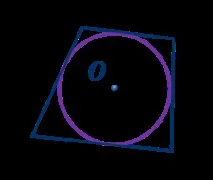
Във всеки описан четириъгълниксумите на противоположните страни са равни.

Акосумата на противоположните странина изпъкнал четириъгълникса равни на, тогаваокръжностможе да бъде вписана в него.

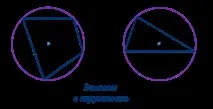
Ако всички върхове на многоъгълника лежат на окръжност, тогава се казва, че окръжността е описана близо до многоъгълника, а многоъгълникът се нарича вписан в тази окръжност.

Теорема.Окръжност може да бъде описана около всеки триъгълник.

Забележки.

1. В близост до всеки триъгълник може да бъде описана самоеднаокръжност.

2. За разлика от триъгълника, не винаги е възможно да се опише окръжност около четириъгълник.

Ако окръжност може да бъде описана около четириъгълник, тогава нейните ъгли имат следното забележителносвойство:

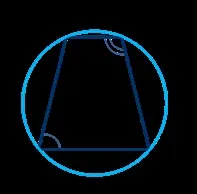
Във всеки вписан четириъгълник сумата от срещуположните ъгли е.

Акосумата от противоположните ъглина четириъгълника е , тогаваоколо негоможетеопишете окръжност.

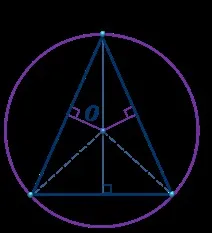
Перпендикулярите, възстановени към средите на страните на триъгълника (перпендикулярни ъглополовящи), се пресичат в една точка, която ецентърът на описаната окръжности се нарича ортоцентър.

Успоредник и трапец. 6

Правоъгълник, ромб, квадрат. 9

Площта на многоъгълника. 13

Площи на успоредник, триъгълник и трапец. 14

Питагорова теорема. 16

Дефиниция на подобни триъгълници. 18

Признаци за подобие на триъгълници. 20

Приложение на подобието при доказване на теореми и решаване на проблеми. 22

Връзки между страни и ъгли на правоъгълен триъгълник. 24

Допирателна към окръжност. 26

Централни и вписани ъгли.. 28

Четири прекрасни точки на триъгълника. тридесет

---