Чубарова Л

Намиране на решения на различни проблеми с помощта на модели в програмата Live Geometry

Светът около нас е свят на геометрия,чист, истински, безупречен в нашите очи.Всичко е геометрия.

Льо Корбюзие

Преподаването на математика беше и все още не е лесна задача. Днес компютърът се превърна във верен помощник на учителя в процеса на преподаване не само на математика, но и на други предмети. Той просто прави чудеса, използвайки огромните си способности. Момчетата обичат да общуват с него, възрастните с готовност му поверяват трудни задачи. Към днешна дата са създадени много различни програми за обучение. Те включват компютърната програма "Жива геометрия".

В "Geometry на живо" всички геометрични форми "оживяват", могат лесно и просто да се променят, копират, рисуват. Децата, използвайки възможностите на "Живата геометрия", самостоятелно започват да забелязват закономерности, да излагат хипотези и да правят първите си открития в математиката. Тази програма, като среда за програмиране, трябва да се мисли, за да се получи резултат.

Тази програма е безценна от първите стъпки в изучаването на геометрията. Упражняване на умения за обозначаване на геометрични обекти (ъгъл, лъч, линия,сегмент), измерване на ъгли, сегменти, сравнение на геометрични фигури, които могат да се извършват не мислено, както е предложено в учебника, а всъщност, като се използват възможностите на компютъра. Всички тези действия са прости и ясни.

Геометрията без теореми е немислима. Но как да "съживим" тези "мъртви" теореми, да ги направим визуални, запомнящи се. Всичко е много просто, ако моделирате теорема с учениците, само в същото време тя ще промени ранга си за известно време: ще се превърне в хипотеза.

Специално място в геометрията заемат строителните задачи, които са трудни за тяхното решение, конструкция. В урока обикновено се отделя много време за такива задачи, качеството на конструкциите на учениците е много ниско (компасът не се подчинява, чупи се, моливът е тъп, линията е удебелена). Съвсем друг е въпросът, ако такива задачи се решават в Живата геометрия. Всички измервания стават точни, конструкциите са бързи и учениците се интересуват само от алгоритъма за решаване на проблема, който след това се проверява с промени в първоначалните данни.

По-високо ниво е изграждането на сценарии в „Геометрия на живо“, които могат да се изпълняват с ученици от 8-9 клас и да се включват с допълнителни обекти в стаята за подготовка.

"Живата геометрия" е предназначена главно за планиметрия, но в нея можете перфектно да демонстрирате задачите на стереометрията за конструиране на сечения от полиедри, да промените условията, при които се изгражда секцията.

Възможностите на "Жива геометрия" не се изчерпват с това. Учителят отново се нуждае от него при решаване на текстови задачи за екстремум в 11 клас. Тези задачи са сред най-трудните в 11. клас, така че използването на модели за такива задачи ги прави по-нагледни и следователно достъпни като решение.

Днес ще представя на вашето внимание модели на няколко задачи от различни дялове на математиката, коитоще покаже нагледно възможностите на тази интересна програма Live Geometry http://iktk.edurm.ru/files/File/metodmat/1.exe.

Строителни задачи

Задачи за конструиране на най-старите геометрични задачи, които също се разглеждат в училищния курс по геометрия. Има много трудности при решаването на такива проблеми: 1) намиране на начин за решаване на проблема чрез установяване на връзки между необходимите елементи и данните на проблема, 2) извършване на конструкцията, 3) доказване на правилността на извършените конструкции, 4) изучаване на проблема, т.е. изясняване на въпроса дали за някакви данни проблемът има решение и ако има, колко решения. Следователно в уроците по математика не се решават толкова много такива задачи. И самият процес на изграждане с молив, линийка, пергел е много неточен. Друго нещо е решението на такива проблеми в компютърната програма "Live Geometry", в която винаги е възможно да се изгради модел за такива проблеми.

Задача 1. Построете окръжност с даден радиус AB, допирателна към дадена права и дадена окръжност с радиус CD.

Нека изградим модел за този проблем и да го използваме, за да разберем дали този проблем винаги има решение.

Ако разстоянието от даден кръг до дадена права линия е 2AB + CD, тогава тази ситуация е показана в модела по-долу.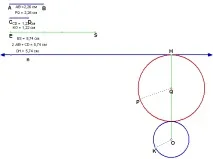

Нека увеличим радиуса на желания кръг, моделът ще приеме различна форма с два кръга, всеки от които удовлетворява решението на задачата.

Ако разстоянието от дадената окръжност до правата е по-голямо от 2AB + CD , то задачата няма решение. Моделът изглежда така.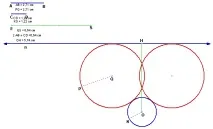

Задача 2. Даден е остроъгълен триъгълник ABC. В него впишете квадрат, чиито два върха лежат на страната AC.

С помощта на модела ще разберем защо в условието на задачата триъгълникът ABC се счита за остроъгълен.

Задача 3. На дадена права лежат точки A, B, C. Намерете множеството от всички точки, за всяка от които отсечките AB и BC се виждат под един и същ ъгъл.

Полученият GMT се нарича кръгът на Аполоний.

Задача 4. Точки A, B, C, D лежат на тази права. Построете точка на равнината, от която отсечките AB, BC и CD се виждат под един и същи ъгъл.

Нека разберем дали проблемът винаги има решение в този случай. Моделът ще ни помогне с това.

1. Ако BC>AB и BC> CD , тогава проблемът в този случай няма решение. Моделът в този случай изглежда така.

Проблемът също няма да има решение, ако AB >BC > CD и . Моделът в този случай изглежда така.

2. Ако , то построяваме окръжността на Аполоний за отсечките BC и CD и след това от точка B възстановяваме перпендикуляра към отсечката AC. С помощта на модела ще разберем дали проблемът винаги има решение.

Може да се види от модела, че ако BC > CD , то окръжността на Аполоний не пресича ъглополовящата на отсечката AC , т.е. проблемът няма решение.