Дефиниция на множеството от минимални покрития

На този етап от множеството максимални кубове, които не принадлежат към ядрото на покритието, се избират такива минимални подмножества, с помощта на всяко от които се покриват останалите върхове (непокрити от ядрото). Препоръчително е този етап да се приложи с помощта на опростена таблица за покритие (Таблица 6). Той зачеркна всички кубове, принадлежащи на ядрото, и върховете, покрити от ядрото.

За решаване на проблема на третия етап може да се използва един от трите метода или комбинация от тях:

1) прост метод на изброяване;

2) метод на Петрик;

3) допълнително опростяване на таблицата за покритие.

Опростена таблица за покритие

Макс кубчета	Значителни върхове
А	000X	´	´
б	X000	´
° С	0X01	´	´
д	01X1	´	´
д	X111	´	´
Е	111X	´
а	b	° С	д	д

На този етап е препоръчително да се въведе обозначението на максималните кубове и съществените върхове.

Максималните кубчета са посочени в табл. 6 главни буквиA, . Fи основни върхове с малки буквиa, . д.

Целесъобразно е методът да се използва за опростена таблица с малък обем. Това не гарантира, че ще бъдат получени всички максимални покрития.

За разглеждания пример всички кубове, включени в опростената таблица на покритията, имат еднакъв размер, т.е. необходимо е да се избере минималният брой от тези кубове, за да покрият всички останали значими върхове.

От табл. 6 показва, че минималният брой кубчета е три. Към възможните минимални опции за покритиеотнасям се:

Методът на Петрик се основава на компилирането на булев израз, който определя условието за покриване на всички основни върхове на булева функция от опростена импликантна таблица. Булевият израз е конюнкция на дизюнктивни термини, всеки от които включва набор от всички прости импликанти, покриващи един основен връх на функцията. Полученият израз се трансформира в дизюнктивна форма и се минимизира с помощта на законите на абсорбцията и тавтологията. Всеки съчинителен член на разделителната форма съответства на една от опциите за покритие, от които се избира минималната.

Предимството на метода на Петрик е получаването на всички минимални покрития.

За разглеждания пример, булев израз, който определя условието за покриване на всички основни върхове в съответствие с табл. 6 ще изглежда така:

Този израз е представен в съчинителна форма. За да се трансформира в дизюнктивна форма, се извършва двойно логическо умножение на дизюнктивни термини.

Забележка.За да се опрости стъпката на преобразуване на изразаYколкото е възможно повече, термините, съдържащи максималния брой букви, се умножават.

След логическото умножение на първите две двойки дизюнктивни членове, получаваме израза:

Y = (AAÚACÚABÚ BC)(CDÚCEÚDDÚDE)(EÚF),

което след прилагане на законите на тавтологията и абсорбцията се свежда до формата:

След логическото умножение на последните две скоби и последващото опростяване получаваме:

Логически умножавайки останалата двойка скоби, получаваме изразаYв дизюнктивна форма:

Y =ADEÚ ADFÚ ACEÚBCDEÚ BCDFÚ BCCE=

=ADEÚ ADFÚ ACEÚBCEÚ BCDF.

Всеки от петте конюнктивни термина съответства на покритието на булевата функция (като се вземе предвид допълнениетоядро), всяко от които може да бъде свързано с DNF в задънена улица.

Последният член не отговаря на минималното покритие, тоест тази функция има четири минимални покрития.

За всички минимални покритияS a =11; S b =15.

Минималните DNF, съответстващи на тези покрития, са:

MDNF1:

MDNF2:

MDNF3:

MDNF4:

Допълнително опростяване на таблицата за покритие е прилагането на две операции:

а) изтриване на "допълнителни" линии;

б) заличаване на „допълнителни“ колони.

Операциите за изтриване на редове и колони се основават на следните правила:

§ ако наборът от етикети наi-ия ред е подмножество от етикети наj-ия ред и кубътiняма по-голямо измерение от кубаj, тогаваi-ият ред може да бъде изтрит от таблицата, тъй като основните върхове, обхванати отi-тия куб, ще бъдат покрити с гаранция отj-ти куб;

§ ако наборът от етикети наk-тата колона на таблицата с покритие е подмножество от етикетите наl-та колона, тогаваl-та колона може да бъде изтрита от таблицата с покритие, тъй като същественият връхlсъс сигурност ще бъде покрит от един от кубовете, покриващ оставащия съществен връхk.

Нека приложим метода за по-нататъшно опростяване на таблицата с покрития по отношение на таблицата. 6. Използвайки операцията за изтриване на „допълнителни“ редове, два редаB иF могат да бъдат премахнати от него, наборът от знаци, в който е подмножество от знаци в редоветеA иE, съответно. Процесът на премахване на „допълнителни“ линии е показан в таблица. 7.

След изтриването на редоветеB иF, съответстващи на максималните кубове X000 и 111X, ще получим нова опростена таблица за покритие, представена под формата на таблица. 8. За разлика отот табл. 6 (опростена таблица на покрития от порядък нула) ще се нарича Таблица. 8 с опростена таблица за покритие от първи ред.

В табл. 8, можем да изберем ново ядро ​​на покритиеT 1 (f)=, което ще наречем ядро ​​на покритие от първи ред, за разлика от ядротоТ(f)(ядро на покритие от нулев ред),, избрано според оригиналната таблица на покритие (Таблица 5).

Зачеркване на "допълнителни" линии

Макс кубчета	Значителни върхове
А	000X	*	*
б	X000	*
° С	0X01	*	*
д	01X1	*	*
д	X111	*	*
Е	111X	*
а	b	° С	д	д

Опростена покриваща маса от първи ред

Макс кубчета	Значителни върхове
0000	0001	0111	1111
А	000X	Ä	*
° С	0X01	*	*
д	01X1	*	*
д	X111	*	Ä
а	b	° С	д	д

След изтриване на кубовете на ядротоT 1 (f)(редовеA иE ), както и основните върхове, покрити от кубовете на ядрото (колониa, b, d, e ), получаваме опростена таблица с покрития от втори ред (Таблица 9).

Опростена таблица за покритие от втори ред

Макс кубчета	Значителни върхове
° С	0X01	*
д	01X1	*

От табл. 9 определя двеминимални покрития под формата на два възможни варианта на допълване на кубовете от ядра на покритието от нулаT (f)и първи редT 1 (f)с кубовеC иD съответно.

По този начин, използвайки метода за опростяване на таблицата с покритие, бяха получени само две минимални покрития:

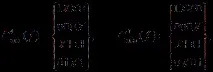
докато методът на Петрик беше използван за намиране на четири минимални покрития, т.е. всички възможни варианти.

---