ДОПЪЛНИТЕЛНИ ПРЕДИЗВИКАТЕЛСТВА И РЕШЕНИЯ

Задача 4.1.DOP

Пълзяща средна = ∑Търсене през предходни n периода / n

Продажбите на велосипеди за фирмата са показани в средната колона на следващата таблица. Средната стойност за три седмици е поставена в дясната колона.

Задача 4.2.DOP

Претеглена пълзяща средна = [∑ (Тегло за период n) *

* (Търсене в период n)] / ∑ Везни

Фирмата се нуждае от прогноза за продажбите на велосипеди, претеглена през последните три седмици, както следва:

Триседмичната претеглена пълзяща средна е поставена по-долу.

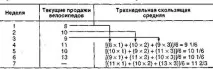
Задача 4.3.ADOP

Задача 4.4.DOP

MAD = ∑ Отклонения / n ;2.5 заа=.8; 2.7 заa=.5.

Въз основа на този анализ изглаждащата константаa -.8 е за предпочитане предa= .5, тъй като дава по-нисък MAD.

Задача 4.6.DOP

Като използвате данните за продажбите по-долу, определете:

а) регресионно уравнение на най-малките квадрати;

б) обем на продажбите през 1993г

Минимизирайки изчисленията, трансформираме стойносттаx(време) в най-простото число. В този случай 1986 ще бъде посочена като година 1, 1987 като година 2 и т.н.

== 28 / 7 = 4; == 917 / 7 = 131;

b = = = 203 / 28 = 10,82,

a = – b = 131 – (10,82) (4) = 87,72.

Така регресионното уравнение изглежда така:

y = 87,72 + 10,82x.

Проектът за търсене през 1993 г., т.е. годинаx =8, ще бъде определен, както следва:

87,72 + 10,82 (8) = 174,28.

Задача 4.10.DOP

Можем да намерим математическото уравнение с помощта на метода на най-малките квадрати.

== 184 / 8 = 23; ==80/8 = 10;

b = = = 0,395,

a = – b = (10 – (0,395) (23) = 0,91.

Така регресионното уравнение изглежда така:

.91 + .395 (30) = 13 апартамента.

Задача 4.11 .DOP

ОПЦИЯ

За задача 4.10.DOP със следните данни:

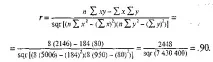
Σх = 184; ;Σх 2 = 5006;Σ y = 80;Σy 2 = 950; 3Σ6xy = 2146; n = 8 изчислете коефициента на корелация.

Този коефициентr =.90 означава значителна корелация и потвърждава връзката между двете променливи:xиy.

Задача 4.14.DOP

Прогнозата за търсенето и текущото търсене на лодки е показано в таблицата по-долу. Въз основа на него изчисляваме проследяващия сигнал и MAD.

Глава 5

Опашките са важна част от глобалното оперативно управление. В тази глава ще представим проблеми на редица системи за масово обслужване и математически модели за техния анализ.

Моделът, илюстриран с едноканална еднофазна система с разпределение на Поасон на появата на рекламации и експоненциално време за обслужване, е модел А; модел B е многоканален еквивалент на модел A; модел C се характеризира с постоянно време на обслужване; модел D - с ограничен размер на източника на приложения. И четирите модела са свързани с разпределението на Поасон на заявките, дисциплината за обслужване „първи влязъл, първи излязъл“ и еднофазно обслужване. Типичните експлоатационни характеристики се считат за средното време на изчакване в опашката и в системата, средния брой приложения в опашката и в системата, времето на празен ход и използването на системата.

Отбелязваме, че има набор от модели за опашка, за които не са изпълнени всички изисквания на традиционните модели. В тези случаи използваме по-сложниматематически модели или методи, наречени симулации на Монте Карло.

ПРОБЛЕМ С РЕШЕНИЯ

Задача 5.1

Компанията наема по един работник всяка година, чиято работа е да товари тухлите на камионите на компанията. Средно на ден преминават 24 камиона, или по три камиона на час, които се появяват според разпределението на Поасон. Работникът ги товари по правилото за четири камиона на час, времето за обслужване се подчинява на експоненциален закон.

Смята се, че вторият товарач ще увеличи значително производителността във фирмата. Мениджърите очакват двама хамали да работят по същия начин: четири камиона на час за един и осем камиона на час за двама. Анализирайте ефекта в опашката от такава промяна и сравнете с резултата, намерен за един работник. Каква е вероятността повече от три камиона да бъдат натоварени или да чакат на опашка?

---