Други" логически и обратими изчисления, SavePearlHarbor
Още едно копие на пристанището
"Друга" логика и обратими изчисления
Започнах да си припомням други примери за създаване на "чужди езици". Например клингонският език от Стар Трек също е базиран на латинската азбука, но е доста добре развит, има собствен синтаксис и речник. Езиците на хората от Средната земя от "Властелинът на пръстените" са съвсем различна история.
Прочетох този цитат от Джеймс Найшин, друг участник в конференцията, професор в Хавайския университет, където се проведе. На сайта му можете да намерите текстовете на две речи, донякъде провокирани от този въпрос: „Как извънземните правят математика” и „Логиката на другите планети”. Може би това не изглежда много сериозно, особено когато различни видове логика се приписват на жителите на различни планети от нашата слънчева система. Въпреки това търсих възможни препратки към една функция, използвана за създаване на обратими порти, и бях изненадан да я открия в неговия раздел за логиката на жителите на Юпитер.
Камък ножица хартия
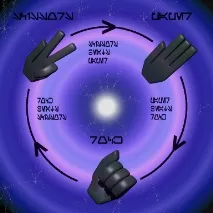
Какво е специалното за "Jovian logic" и как е свързано с обратимото изчисление? Naishin използва набор от три елемента, за да го опише, обозначени със символите R, P, S, които съответстват на първите букви от английските думи за камък, ножици и хартия. Играта "камък, ножици, хартия" (за нея също е писано тук повече от веднъж) е известна на Хаваите и като "jiang-ken". Според правилата на игратаедин от трите елемента побеждава другия въз основа на цикличен набор от предпочитания. Това обикновено се показва на кръгова диаграма, но може да бъде написано и на линия:
S на обикновената логика. И така, установяването на връзки между елементи дефинира аналози на логическите операции. Вярно е, че с цикличен набор от предпочитания между три елемента някои свойства трябва да бъдат пожертвани. Какво да се прави, друга логика.
Таблицата за аналога "ИЛИ" с този подход изглежда така
| Друго ИЛИ | Р | П | С |
| Р | Р | П | Р |
| П | П | П | С |
| С | Р | С | С |
Таблицата за операцията "И" е подобна
| Други И | Р | П | С |
| Р | Р | Р | С |
| П | Р | П | П |
| С | С | П | С |
Обратими изчисления
Какво ще кажете за обратимите изчисления? За тях вече е писано тук, както и, между другото, за троичната логика (тук, в geektimes, повече тук) и дори се опита да ги обедини.
Обратимите порти могат да бъдат полезни за решаване на проблема с разсейването на топлината в процесорите от следващо поколение, те са тясно свързани с теорията на квантовите изчисления. А самата тема е доста интересна. Можете да прочетете за това на много места, включително връзките по-горе, така че ще се опитам да не разширявам много темата за вече доста добре известни неща.
Накратко, портата е обратима, когато стойностите на входовете винаги могат да бъдат възстановени от стойностите на изходите. Универсалните портове обикновено се използват за работа с двоични данни.Тофоли или Фредкин. И двата порта имат три входа и три изхода, тъй като, за разлика от необратимия случай, е невъзможно да се създаде набор от обратими двоични порти с два входа за извършване на произволна операция върху данни.
Нека се опитаме да си представим обратим аналог на обичайната порта "ИЛИ". Да предположим, че има два входа (и два изхода, тъй като трябва да е обратим), входовете са двоични стойности и един от изходите трябва да даде резултата от операцията "ИЛИ". Оказва се, че същата стойност 1 (TRUE) на този изход може да бъде получена с три различни комбинации на входа: 11, 01, 10. Ако вторият изход може да има три различни стойности, това може да се използва за обръщане на такъв гейт.
И така, вече доста прости оценки водят до идеята за използване на троичната система поне на един изход. Но какво ще стане, ако се опитате да работите с три стойности на всички входове и изходи - възможно ли е да получите обратима порта, ако използвате троична логика?
Доста често срещана е троичната логика на Лукасевич. Може да се конструира и чрез трика с максимум и минимум, вече споменат по-горе, ако приемем, че третата стойност съответства на някакво число x, 0 00 01 0x 10 11 1x x0 x1 xx и тъй като портата е обратима, тогава всяка от тези девет двойки трябва да се появи на изхода с една от комбинациите на входа. Може да се види, че в тези двойки всяка стойност на първия (и втория) елемент ще се появи три пъти.
Тоест три нули, три единици, три х-та. И вместо това в таблицата за троичното "ИЛИ" има само една нула и шест единици. Във втората таблица за "И", напротив, има шест нули и една единица, което също не е подходящо.
Следователно, въпреки че обратимите троични порти отделно и троичната логика отделно са доста широко разпространенисе използват, е трудно да се съберат заедно. Тук идва на помощ "извънземната" логика. За по-голяма яснота заместваме R,P,S с 0,1,$.

Ето таблицата за "ИЛИ"
| „Друго ИЛИ“ | 0 | 1 | $ |
| 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | $ |
| $ | 0 | $ | $ |
За стойностите 0, 1 е същото като обичайното "ИЛИ", но в същото време има вече споменатото свойство, необходимо за създаване на обратима троична порта (всяка стойност се среща три пъти). Подобна е ситуацията с таблицата за операцията "И".
| "Друго И" | 0 | 1 | $ |
| 0 | 0 | 0 | $ |
| 1 | 0 | 1 | 1 |
| $ | $ | 1 | $ |
Сега, за да изградим пълна версия на обратими троични порти, ние също трябва да изберем таблица за втория, спомагателен изход. В обикновената аритметика b–a може да се използва за обръщане на функцията max(a,b) на втория изход. Нещо подобно може да се използва в нашия пример
| "Още една разлика" | 0 | 1 | $ |
| 0 | 0 | $ | 1 |
| 1 | 1 | 0 | $ |
| $ | $ | 1 | 0 |
Появи се - така ще изглежда пълна тройна обратима порта "ИЛИ".
| Вход | 00 | 01 | 0$ | 10 | единадесет | 1$ | $0 | $1 | $$ |
| Изход | 00 | единадесет | 0$ | 1$ | 10 | $1 | 01 | $$ | $0 |
Може да се види, че всяка от деветте възможни комбинации се появява веднъж в изхода, така че операцията е обратима. Работата на тази порта може да се опише и по следния начин: тя не променя двойките 00, 0$, като пермутира седем двойки (01, 11, 10, 1$, $1, $$, $0) в цикъл
И така, прилагането на портата седем пъти ще остави всяка двойка стойности непроменена, а обратната операция съответства на прилагането на шест порти подред. По-просто е с портите на Тофоли и Фредкин, всяка от тях съвпада с обратната си.
Ако към входа се прилагат само стойностите нула и едно, тогава тази троична порта изпълнява обичайната логическа операция "ИЛИ". Като зададете втория вход на едно, можете да използвате втория изход като операция "НЕ" от първия вход. В допълнение, портата изпълнява операцията на "разклоняване" на двоичната стойност, подадена към втория вход, ако към първия е приложена нула. Така че този обратим троичен гейт е универсален за работа с двоични данни.
Пример за обратима троична "И" врата е подобен
| Вход | 00 | 01 | 0$ | 10 | единадесет | 1$ | $0 | $1 | $$ |
| Изход | 00 | 01 | $$ | 0$ | 10 | единадесет | $1 | 1$ | $0 |
Тази порта не променя двойките 00 и 01, разменяйки двойките (0$, $$, $0, $1, 1$, 11, 10, 0$)
Той също е универсален за двоични операции, но за разлика от "ИЛИ", един такъв гейт не е достатъчен за "разклоняване". Вярно, изборът на операция на втория изход беше доста произволен. Операцията на първия вход се определя еднозначно от избора на три условия: (1) изпълнижеланата логическа операция за двоични данни, (2) съответстват на една от входните стойности, (3) не зависят от тяхната пермутация.
Изборът на работа на първия вход също е съвсем естествен и може да се използва и за други модели. Да предположим, че трябва да изградим обратима врата за логиката на Лукасевич. Проблемът с това вече е описан, някои стойности се появяват в таблицата 3x3 пет пъти и те трябва да са равни, за да се направи реверсивна врата.
Още гущер и Спок
Тук можете да приложите същата идея като при разширяване на двоичната логика към система от три елемента и въз основа на съществуващия проблем с пет повторения в таблицата за троичната логика на Лукасевич (0, 1, x), трябва да добавите още два елемента ($ и @). Друг аргумент в полза на петте стойности е свързан с използването на аналога на разликата b-a за обръщане на максимума и минимума: разликата между три цели числа от 0 до 2 може да приеме пет различни стойности от -2 до 2.
Отношенията между елементите отново могат да бъдат изобразени на кръгова диаграма или записани в ред 0 Съответната игра също е известна. Например нейната версия беше показана в поредицата "Теория за Големия взрив" (снимка с обяснение). Съответствията могат да бъдат избрани както следва: 0 - камък, 1 - хартия, $ - ножица, @ - гущер, x - Спок (родом от планетата Вулкан в поредицата Стар Трек).

Можете да продължите и още; за подобни кръгови диаграми, наборите, които имат прост брой елементи, са особено подходящи.
Колективна логика и "невъзможни стрели"
Трябва да кажа, че цикличната логика не е толкова „чужда“. Един от най-характерните примери е свързан с парадоксите на Кондорсе и Ароу, свързани с проблема за избора. Типично описание на "парадокса на гласуването"можете да намерите в книгата "Колективен избор и индивидуални ценности" на Нобеловия лауреат по икономика Кенет Ароу.
Да разгледаме избор от три алтернативи (например избори с трима кандидати) A, B, C. В същото време всеки избирател има определена подредена система от предпочитания. Тоест, ако първата алтернатива е за предпочитане пред втората, а втората е за предпочитане пред третата, тогава първата е за предпочитане и пред третата. Пример за проблеми с подбора, които възникват, когато този критерий е нарушен, също е описан по-долу.
Такива подредени предпочитания са пример за транзитивни отношения, а операциите с подобно свойство са асоциативни, тоест не зависят от подреждането на скоби. Обсъдената по-рано дефиниция на операцията ИЛИ по отношение на уточняване на връзките на елементите се вписва добре в идеята за избор: операцията "А ИЛИ Б" е просто избор между А и Б, базиран на някакъв набор от предпочитания (включително случая "А ИЛИ А", който, въпреки че е трудно да се нарече "избор", също има добре дефиниран резултат, А).
Нека някой вярва, че B е по-добро от A, C е по-добро от B (и по критерия, даден по-рано, C е по-добро от A). Записваме този избор като (1) A ((A B) C) = B C = C, (A (B C)) = A C = A