Двупосочен детерминистичен краен автомат
| Определение: |
Двупосочен детерминистичен краен автомат (2DFA)— набор от осем елемента [math]M = \langle \Sigma , Q, L, R, s, t, r, \delta \rangle[/math] , където
|
Трябва също така да бъдат изпълнени следните условия:
[math]\forall q \in Q[/math]
- [math]\delta(q, L) = (u, дясно)[/math] за някои [math]u \in Q[/math],
- [math]\delta(q, R) = (v, ляво)[/math] за някои [math]v \in Q[/math],
и [math]\forall b \in \Sigma \cup \[/math]
- [math]\delta(t, b) = (t, right)[/math] ,
- [math]\delta(r, b) = (r, right)[/math] ,
- [math]\delta(t, R) = (t, ляво)[/math] ,
- [math]\delta(r, R) = (r, ляво)[/math] .
Съдържание
Езикова редовност[редактиране]
Помислете за дълъг входен низ [math]w_1[/math] и го разделете на два подниза [math]w_1=xz[/math] . Да приемем, че [math]w_1 = a_1 a_2 a_3 \dots a_n[/math] . Нека [math]a_0 = L[/math] и [math]a_=R[/math] . Тъй като имаме нашата машинаможе да чете във всяка посока, границата между [math]x[/math] и [math]z[/math] може да бъде пресичана многократно. Всеки път, когато автоматът пресича границата отдясно наляво (т.е. от [math]z[/math] към [math]x[/math]), той преминава от [math]z[/math] в състояние [math]q[/math]. Когато пресичането се случи отново отляво надясно (ако изобщо се случи), тогава автоматът излиза [math]x[/math] в състояние [math]p[/math] . Сега, ако 2DFA отново премине в състояние [math]x[/math], тогава може отново да се появи в състояние [math]p[/math]. Освен това, състоянието на [math]p[/math] зависи единствено от [math]q[/math] и [math]x[/math] . Нека обозначим тази връзка като [math]T_x(q) = p[/math] . Можем да напишем всички такива отношения под формата на крайна таблица [math]T_x : Q \cup \ \to Q \cup \[/math] , където [math]Q[/math] е набор от 2DFA състояния, а [math]d[/math] и [math]h[/math] ще бъдат описани по-долу.
На входния ред [math]xz[/math] 2DFA ще започне да чете от левия маркер за край на реда. По време на работа на машината позицията за четене ще се промени. В крайна сметка тази позиция ще пресече отляво надясно границата между [math]x[/math] и [math]z[/math] . Първият път, когато това ще се случи, е в някакво състояние, което ще наречем [math]T_x(d)[/math] (затова сме избрали [math]d[/math]). Освен това автоматът може никога да не излезе от [math]x[/math] . В този случай пишем [math]T_x(d) = h[/math] . Състоянието [math]T_x(d)[/math] дава известна информация за [math]x[/math], но само ограничено количество, тъй като има само краен брой опции за [math]T_x(d)[/math]. Имайте предвид, че [math]T_x(d)[/math] зависи само от [math]x[/math] и не зависи от [math]z[/math] . Ако входът ще бъде низът [math]xw[/math] вместо [math]xz[/math], тогава вВ този случай, когато пресича границата от [math]x[/math] към [math]w[/math], автоматът също ще бъде в състояние [math]T_x(d)[/math], тъй като стойността му до този момент се определя само от [math]x[/math] и дотогава всичко, което е вдясно от границата, няма ефект.
Ако [math]T_x(d) = h[/math], тогава 2DFA е в безкраен цикъл вътре в [math]x[/math] и никога няма да приеме или отхвърли входния низ.
Да предположим, че 2DFA преминава от [math]x[/math] към [math]z[/math] и след известно време се връща към [math]q[/math] . Ако това се случи, тогава:
- или отново ще има преход от [math]x[/math] към някакво състояние [math]p[/math] . В такъв случай ние дефинираме [math]T_x(q)=p[/math] .
- или никога да не се движи. В такъв случай [math]T_x(q) = h[/math] .
Обърнете внимание отново, че [math]T_x(q)[/math] зависи само от [math]x[/math] и [math]q[/math] и не зависи от [math]z[/math]. Ако автоматът премине към [math]x[/math] отдясно в състояние [math]q[/math], тогава той ще се появи отново в състояние [math]T_x(q)[/math] (или никога не преминава, ако [math]T_x(q) = h[/math] ), тъй като автоматът е детерминистичен и поведението му се определя напълно от [math]x[/math] и състоянието, в което е влязъл.
Ако запишем [math]T_x(q)[/math] за всяко състояние [math]q[/math] заедно с [math]T_x(d)[/math], това ще ни даде цялата информация за [math]x[/math], която може да бъде пренесена през границата между [math]x[/math] и [math]z[/math]. Всичко това ще ви позволи да разберете [math]T_x(d)[/math] веднага след преминаване на границата, както и да видите стойностите на [math]T_x(q)[/math] . Ако [math]y[/math] е друг низ, така че [math]T_y=T_x[/math], тогава [math]x[/math] и [math]y[/math] ще бъдат неразличими.
Имайте предвид, че имаме краен брой възможни таблици [math]T_x : Q \cup \ \to Q \cup \[/math] , а именно [math](k+1)^[/math] , където [math]k[/math] е размерът на набора [math]Q[/math]. По този начин имаме ограничено количество информация за [math]x[/math], която можем да пренесем над границата отдясно на [math]x[/math] и която е кодирана в нашата таблица [math]T_x[/math].
Обърнете внимание също, че ако [math]T_x=T_y[/math] и автоматът приема низа [math]xz[/math], тогава той приема и низа [math]yz[/math], тъй като последователността от състояния, пренесена над границата на [math]x[/math] и [math]z[/math] (или [math]y[/math] и [math]z[/math] ) във всяка посока се определя напълно от таблиците [math]T_x=T_y[/math ] и низа [math]z[/math] . За да приеме низа [math]xz[/math], автоматът трябва в даден момент да прочете десния маркер за край на реда, докато е в състояние на приемане [math]t[/math] .
Вече можем да използваме теоремата на Myhill-Nerode, за да покажем, че езикът [math]L(M)[/math] на нашия автомат [math]M[/math] е правилен.
[math]T_x = T_y \Rightright\forall z (M\ \text\ xz \Leftrightarrow M\ \text\ yz)[/math] \Leftrightarrow \forall z (xz \in L(M)[/math] [math] \Leftrightarrow yz \in L(M)) \Leftrightarrow x \equiv_ y[/math] , където [math]\equiv_[/ math] е отношението на еквивалентност на много думи в азбуката. По този начин, ако 2 реда имат еднакви таблици, тогава те са еквивалентни чрез релацията [math]\equiv_[/math] . Тъй като имаме само краен брой таблици, релацията [math]\equiv_[/math] има само краен брой класове на еквивалентност, най-много един за всяка таблица. Следователно, според теоремата на Myhill-Nerode, [math]L(M)[/math] е нормален език, който според теоремата на Kleene е същият катоклас и автоматични езици и др.
Пример[редактиране]
Разгледайте следния език [math]L_n = (a+b)^∗a(a+b)^a(a+b)^∗[/math] с [math]\forall n \gt 0[/math] .
Може лесно да се разпознае със следната недетерминирана държавна машина.
Сега нека изградим DFA на негова основа. Можем да изградим автомат [math]A_n[/math], който помни последните [math]n[/math] въведени знаци. Следователно, когато сме в състояние, съответстващо на подниза [math]\sigma_1 \sigma_2 \dots \sigma_n[/math] и прочетем следващия знак [math]\gamma[/math] , тогава отиваме в състоянието, на което поднизът [math]\sigma_2 \sigma_3 \dots \sigma_n \gamma[/math] вече ще съответства. Въпреки това, в случай на [math]\sigma_1 = \gamma = a[/math] автоматът преминава в приемащо състояние, където може да отиде до всеки знак в цикъла. Трябва да се отбележи, че такава стратегия изгражда DFA с [math]2^n + 1[/math] състояния. По-долу е автоматът [math]A_3[/math] , който разпознава езика [math]L_3[/math] .
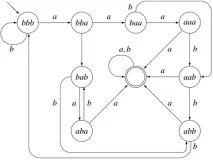
Нека покажем, че конструираните по този начин автомати са минимални.
- Всеки два по двойки различни низа [math]x[/math] и [math]y[/math] с дължина [math]n[/math] са различими. За да докажете това, достатъчно е да разгледате реда [math] b^a [/math], където [math] i: 1 \ leqslant i \ leqslant n [/math] е лявата позиция на символа, в която редовете [math] x [/math] и [math] y започват да се различават, и да проверите дали точно един ред [make] xb ^a [/math] или [math] yb^a [/math] принадлежи s към [math] l_n [/math].
- Всеки низ с дължина [math]n[/math] не принадлежи на [math]L_n[/math] и следователно се различава от низа [math]a^[/math] , който принадлежи на[math]L_n[/math] .
- Така [math]2^n + 1[/math] редове в [math]\Sigma^n \cup \\>[/math] са различими по двойки за [math]L_n[/math] . Като следствие, [math]2^n + 1[/math] е минималният брой състояния за DFA, който може да разпознае езика [math]L_n[/math] .
За да определите, че низът [math]w=c_1 \dots c_n[/math] принадлежи на езика [math]L_n[/math], трябва да проверите за [math]\forall i = 1, \dots, w-n[/math], че [math]c_i=c_=a[/math] . Низът ще бъде валиден, ако условието е вярно за поне един [math]i[/math] . Този алгоритъм може лесно да се реализира с помощта на 2DFA. За всеки [math]i[/math] ще се преместим напред [math]n[/math] позиции и след това [math]n-1[/math] позиции обратно към позиция [math]i+1[/math] . В допълнение, при преместване от позиция [math]i[/math] към [math]i+n[/math] автоматът трябва да помни дали условието [math]c_i=a[/math] се запазва. Този подход изисква [math]O(n)[/math] състояния.