Една права е перпендикулярна на равнина, ако тя
перпендикулярно на две пресичащи се прави
в тази равнина.(17)
Точка A принадлежи на равнината, тъй като принадлежи на правата CD, която от своя страна принадлежи на равнината (14). Проекциите на точка спадат към проекциите на права.
Същата равнина, линия и точка са показани на плоския чертеж на фиг. 13. Фронталната следа на равнината Q2 и нейната челна проекция (Q2)2 съвпадат. Хоризонталната проекция (Q2)1 на челната следа Q2 съвпада с оста X12. Хоризонталната проекция (Q1)1 на хоризонталната следа Q1 съвпада със следата. Фронталната проекция (Q1)2 съвпада с оста X12.
Позицията на равнината в правоъгълната координатна система се определя от позицията на нейната основа A(X, Y, Z) и ъглите на наклона на равнината a, b, g спрямо проекционните равнини.
Ъгъл a на наклона на равнината Q към хоризонталната равнина на проекциите P1 може да се определи чрез промяна на ъгъла на наклон на равнината Q към равнината P2 на 90°. В този случай равнината Q и равнината P1, образуващи двустенен ъгъл, ще бъдат перпендикулярни на третата равнина P2. Съгласно правилото за измерване на двустенен ъгъл (15), той ще бъде определен между пресечната линия на равнината Q с равнината P2 (следа на равнината Q 1 2) и линията на пресичане на равнината P1 с равнината P2 (ос X12).
Равнината Q ще бъде перпендикулярна на равнината P2, ако която и да е линия от равнината Q е перпендикулярна на равнината P2 (16). Освен това ъгълът a на тази права е равен на нула, например прави Q1 и CD. b Q 1 = Q1 Ù (Q1)2 , където (Q1)2 съвпада с X12, b CD = CD Ù С2D2.
В позиция 1 (фиг. 13) въртенето около оста iz (виж фиг. 3) променя ъгъла b на равнината Q на 90°. Защо ъглите b Q 1 и b CD се променят от първоначалната позиция на 90 ° (Q 1 1 ^ X12, C 1 1D 1 1 ^ X12). Разстоянието e, което определя взаимното положение на успоредни правиостава непроменена (когато a = const, геометрията на хоризонталната проекция се запазва).
Фронталната следа на равнината Q 1 2 е построена върху две точки: точката на пресичане на хоризонталната следа Q 1 1 с оста X (следите се пресичат в точка на оста X) и фронталната проекция на точката C 1 2 (точката C принадлежи на фронталната следа на равнината и C 1 2 съвпада с C 1 ). Хоризонталната проекция C 1 1 се намира в пресечната точка на хоризонталната проекция на правата линия CD с оста X, тъй като Y C \u003d 0. Фронталната проекция C 1 2 се намира в пресечната точка на комуникационните линии към оста X и комуникационната линия към оста Z през C2.
Ъгъл b на наклона на равнината Q спрямо фронталната равнина на проекциите П2
може да се определи чрез промяна на ъгъла на наклона на равнината Q към равнината
P1 до 90°. В този случай равнината Q и равнината P2, образуващи двустенен ъгъл, ще бъдат перпендикулярни на третата равнина P1. Ъгълът b Q ще бъде определен между линията на пресичане на равнината Q с равнината P1 и линията на пресичане на равнината P2 с равнината P1.
Пример. Определяне на параметрите на равнината D(ABC) (фиг. 14).
Външни параметри определят позицията на обекта в пространството:
- текуща BT база (X, Y, Z);
- ъгли на наклон a, b и g към проекционните равнини (два ъгъла са достатъчни за практически цели).
Вътрешните параметри определят геометричните размери на обекта. Например дължината на права линия, площта на триъгълник и т.н. Промяната на вътрешните параметри променя свойствата на обекта. Например самолет с променлива геометрия на крилото.
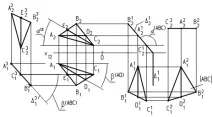 |
За да се определи ъгълът на наклон a на равнината ABC към хоризонталната проекционна равнина P1 в първата текуща позиция, ъгълът b е променен на 90°. Защо взехме правата AD(A1D1,A2D2) в равнината ABC,ъгъл на наклон
който спрямо равнината P1 е равен на 0. Ъгълът на наклон b ( AD ) към P2 се измерва съгласно (6) между (A1D1) = ÷AD÷ и (A2D2). В първата текуща позиция той се увеличава до 90°. В резултат b ( A BC) съгласно (16) е равно на 90°. Фронталната следа на равнината D 1 2 съвпада с фронталната проекция на триъгълника (A 1 2B 1 2C 1 2).
За да се определи ъгълът на наклон b на равнината ABC спрямо фронталната равнина на проекциите P2 в третата текуща позиция, ъгълът a на равнината е променен на 90°. Защо в равнината ABC взехме правата линия CE(C1E1,C2E2), чийто ъгъл на наклон към равнината P2 е равен на 0. Ъгълът на наклон a (CE) към P1 се измерва съгласно (6) между (C2E2) = ÷SE÷ и (C1E1). В третата текуща позиция той се увеличава до 90°. В резултат на това a ( A BC) съгласно (16) е равно на 90°. Хоризонталната следа на равнината D 3 1 ще съвпадне с хоризонталната проекция на триъгълника (A 3 1B 3 1C 3 1).Съгласно (15), ъгълът на наклонb (ABC) \u003d D 3 1 (линията на пресичане на равнината ABC с P1) ÙX12 (линията на пресичане на равнината P 2 с P1).
За да се определи естествената стойност на D(ABC) в текущата позиция, ъгълът на наклонa (ABC) чрез въртене около оста iY (вижте Фиг. 3) се променя на 0. В този случай хоризонталната проекция на триъгълника (A 2 1B 2 1C 2 1) = ÷ABC÷. Само в тази позиция на плосък чертеж можете да промените вътрешните геометрични параметри на триъгълника и да извършите други геометрични конструкции в равнината D (например да определите височината на триъгълника, да изградите вписан кръг и т.н.).
Взаимна позиция на точките
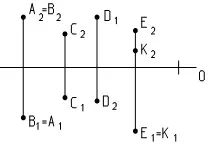
Ориз. 15 проекции.
На фиг. 15 точки A и B съвпадат, тъй като техните фронтални проекции A2=B2 и хоризонталните проекции A1=B1 съвпадат. Точка C е по-далеч от наблюдателя и по-ниско спрямо точка D (координатите Y и Z на точка D са по-големи). Точките E и K са на еднакво разстояние от равнината P2 (Y E \u003d Y K), но точка E е разположена над точка K (Z E е по-голяма от Z K).