Еластично-пластично огъване на греди
В напречните сечения на гредата по време на огъване нормалните напрежения в еластичното състояние на материала се разпределят неравномерно, варирайки линейно по височината на гредата (фиг. а).
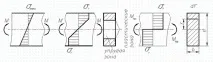
Изчисления на флексия
Най-големите нормални напрежения в най-отдалечените от неутралната линия точки на напречното сечение се определят по формулата
.
При изчисляване на якостта за допустими напрежения границата на безопасност се определя като съотношението на границата на провлачане на материала към най-високото напрежение. Именно за това състоянието на гредата се приема за опасно, което съответства на постигането на най-големи нормални напрежения в опасни участъци от границата на провлачване. Това състояние само условно може да се счита за опасно. Гредата все още запазва способността да възприема огъващия момент, увеличава се.
Нека определим стойността на граничния момент на огъване в случай на чисто огъване. Помислете първо за греда, чието напречно сечение има две оси на симетрия. Границите на провлачване при опън и натиск ще се считат за еднакви.
След появата на течливост в най-отдалечените точки на сечението от неутралната ос, с по-нататъшно увеличаване на огъващия момент, пластичното състояние на материала се разпространява към неутралната ос. До пълното изчерпване на носимоспособността на гредата в напречните й сечения ще има две зони - пластична и еластична (фиг. б). Граничното състояние ще настъпи, когато провлачването се разпространи по цялото напречно сечение, тъй като след това настъпва по-нататъшна деформация на гредата без увеличаване на момента на огъване. Графиката на нормалните напрежения в напречното сечение за гранично състояние е показана на фиг. V . В разглежданото напречно сечение се образува така наречената пластмасова панта, която предава постоянен момент, равен на границатамомент на огъване.
Ограничаващият момент може да се изчисли като сума от моментите около неутралната ос на силите в напречното сечение (фиг. c):
където е статичният момент на площта на половината от напречното сечение около неутралната ос.
Стойността обикновено се нарича пластичен съпротивителен момент и се означава с . Тогава
За правоъгълно напречно сечение с ширина и височина
Опасна стойност на момента на огъване при изчисляване на допустимото напрежение
характеризира степента на увеличаване на границата на безопасност на гредата при прехода към изчисляване на граничното състояние. В случай на правоъгълна греда
За I-гредите се валцуват средно. Ако сечението на гредата има само една ос на симетрия в равнината на товара (фиг. 13.12), тогава в гранично състояние неутралната ос ще премине през центъра на тежестта на напречното сечение.
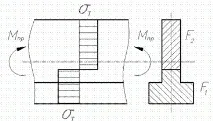
Разрез с една ос на симетрия
Позицията на неутралната ос се определя от равенството до нула на сумата от проекциите върху оста на гредата на всички сили, разпределени върху нейното сечение:
където е площта на зоната на разтегнатия участък;
е площта на компресираната зона.
Оттук получаваме , тоест в гранично състояние неутралната ос на сечението трябва да разделя неговата площ наполовина.
Краен момент на огъване
където е статичният момент на зоната на разтегнато сечение спрямо неутралната ос;
е абсолютната стойност на статичния момент на компресираната зона на сечението по отношение на същата ос.
В този случай пластмасовият момент на съпротива
Горните аргументи относно дефинирането на граничното състояние, което е еквивалентно на образуването на пластичен шарнир в напречното сечение на гредата, строго погледнато, са валидни само за чисто огъване, когато няма напрежения на срязване. Определение на границатасъстояние по отношение на напречната сила е по-трудно. Този въпрос не се разглежда тук.
Помислете за пример за изчисляване на греди за огъване, разрешени за нажежаване и за гранично състояние, без да се отчита влиянието на напречната сила.
Греда с правоъгълно напречно сечение, захваната в краищата, носи интензитет, равномерно разпределен по дължината на товара (фиг. 16.3, а). Определете максималната интензивност на това натоварване, допустима според изчислението на допустимото напрежение и според граничното състояние със същата граница на безопасност.
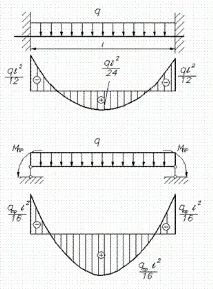
Изчисляване без отчитане на влиянието на срязващата сила
Изчисляване на допустимите напрежения. Гредата е статически неопределена. Изчисляването му е значително опростено поради симетрията. Намираме допълнителни неизвестни и изграждаме диаграма на моментите на огъване (фиг. 16.3, но). Най-голямата стойност на огъващия момент е в захванатите опорни секции:
С увеличаване на натоварването максималните напрежения в същите секции първо ще достигнат границата на провлачване. Като вземем границата на границата на провлачване, равна на , намираме най-високия допустим интензитет на натоварване от условието за якост:
Като се има предвид това, получаваме
Изчисляване на гранично състояние. След появата на пластични деформации в точките на опорните секции, които са най-отдалечени от неутралната ос, по-нататъшното увеличаване на натоварването ще доведе до образуване на пластмасови панти в тези секции и моментът на огъване ще достигне граничната стойност. Сега гредата вече работи като шарнирна опора, към която се прилагат постоянни моменти върху опорите (фиг. 16.3, b)
При по-нататъшно увеличаване на натоварването тези моменти запазват своята стойност и проблемът става статично дефиниран. В участъците на обхвата големината на огъващите моменти ще се увеличи, докато моментът в средата на обхвата стане равен насъщата стойност, т.е. докато се образува пластмасова панта. В този случай три пластмасови панти ще бъдат разположени на една права линия, така че по-нататъшното увеличаване на товара е невъзможно. Носещата способност на гредата ще изсъхне.
Условието за равенство на огъващите моменти в опорните секции и в средата на обхвата има формата
откъде намираме това
Съставяйки правилните части на формули (19.51) и (19.53), намираме:
Приемайки границата на безопасност равна, получаваме най-високата допустима интензивност на натоварване:
Съотношението на най-големите допустими натоварвания при изчисленията за гранично състояние и за допустимото напрежение
.
Анализът на граничното състояние често дава възможност да се разкрият допълнителни якостни резерви. Както бе споменато по-горе, той се използва широко при изчисляването на строителни конструкции.
Изчислението на граничното състояние с определен марж на безопасност не гарантира срещу появата на локални пластични деформации. Последното все още е допустимо при постоянни натоварвания, които се извършват главно в строителни конструкции. При променливи натоварвания, на които най-често трябва да се изчисляват инженерните конструкции, появата на пластични деформации в много случаи е неприемлива. Следователно в такива случаи си струва да се изчислят допустимите напрежения.