Елементи на квантовата механика
59. Докажете, че груповата скорост на вълните на де Бройл е равна на скоростта на свободно движеща се частица. Разгледайте нерелативистичния и релативистичния случай.
60. Докажете, че за частица, която се движи свободно с постоянна скорост v, е в сила отношението vphases u = c2 (u е груповата скорост).
61. Изведете закона за дисперсията на вълните на де Бройл, т.е. зависимостта на фазовата скорост на вълните на де Бройл от тяхната дължина на вълната. Разгледайте нерелативистичния и релативистичния случай.
62. Ширината на следата на електрон (с кинетична енергия T \u003d 1,5 keV) върху фотографска плака, получена с помощта на облачна камера, е Δx \u003d 1 микрон. Определете дали е възможно да откриете отклонение в движението на електрона от законите на класическата механика, като използвате тази следа.

63. Електронен лъч се ускорява в катодна тръба с потенциална разлика U = 1 kV. Известно е, че неопределеността на скоростта е 0,1% от числовата й стойност. Определете несигурността на координатата на електрона. Дали електроните при тези условия са квантова или класическа частица?

64. Определете съотношението на неопределеността на скоростта на електрона, ако неговата координата е зададена с точност от 10 -5 m, и прахова частица с маса m = 10 -12 kg, ако нейната координата е зададена със същата точност.

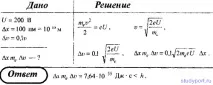
65. Електронният лъч напуска електронната пушка под действието на потенциална разлика U = 200 V. Определете дали е възможно едновременно да се измери траекторията на електрон с точност до 100 pm (с точност от порядъка на диаметъра на атом) и неговата скорост с точност 10%.
66. Електрон се движи във водороден атом по първата орбита на Бор. Ако приемем, че допустимата неопределеност на скоростта е 10% от числената й стойност, определете неопределеността на координататаелектрон. Приложима ли е концепцията за траектория в този случай за електрон?

68. Използвайки съотношението на несигурност във формата Δx Δpx >= h, изчислете минималната възможна обща енергия на електрон във водороден атом. Вземете несигурността на координатата, равна на радиуса на атома. Сравнете резултата си с теорията на Бор.

70. Използвайки съотношението на неопределеността, оценете размиването на енергийното ниво във водородния атом: 1) за основното състояние; 2) за възбудено състояние (времето на живот е 10 -8 s).

71. Дължината на вълната λ на фотон, излъчен от атом, е 0,6 микрона. Приемайки времето на живот на възбуденото състояние Δt = 10 s, определете съотношението на естествената ширина на енергийното ниво, до което електронът е бил възбуден, към енергията, излъчена от атома.

72. Ако приемем, че електронът е вътре в атом с диаметър 0,3 nm, определете (в електронволта) несигурността в енергията на този електрон.
76. Вълновата функция, описваща някаква частица, може да бъде представена като ψ(x, t) = ψ(x)*e –( i/ h)* Et . Покажете, че плътността на вероятността за намиране на частица се определя само от координатната ψ-функция.
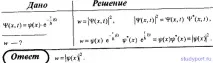
77. ψ-функцията на дадена частица има формата ψ = A/r*e - r/a, където r е разстоянието на тази частица до центъра на силата;aе някаква константа. Като използвате условието за нормализиране на вероятността, определете коефициента на нормализиране A.
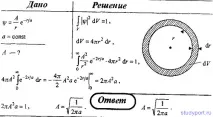
78. Използвайки условието за нормализиране на вероятността, определете коефициента на нормализиране A на вълновата функция ψ = A*е - r/a, описваща основното състояние на електрон във водороден атом, където r е разстоянието на електрона от ядрото,aе първият радиус на Бор.

79. Използванеусловие за нормализиране на вероятността, определя коефициента на нормализиране на вълновата функция ψ(r) = A*e - r^2/(2а^2), описваща поведението на дадена частица, където r е разстоянието на частицата от центъра на силата;aе някаква константа.
80. Вълновата функция ψ = A sin(2πx/l) е дефинирана само в областта 0 - r/a, където r е разстоянието на тази частица до центъра на силата;aе някаква константа. Определете средното разстояние на частицата от центъра на силата.

82. Вълновата функция, описваща дадена частица, има форматаaе някаква константа. Определете средното разстояние на частицата от центъра на силата.

Грешка в текста? Изберете го с мишката и щракнете
Имате ли есета, курсови работи, презентации? Споделете с нас - изтеглете ги тук!