Формула на косинусова теорема, следствия и примери за решения
Формула на косинусовата теорема
Квадратът на една страна на триъгълник е равен на сбора от квадратите на другите две страни минус удвоеното произведение на тези страни по косинуса на ъгъла между тях.
Тоест, за плосък триъгълник (фиг. 1) със страни $a$, $b$ и $c$ и ъгъл $\alpha$ срещу страната $a$, връзката е вярна:
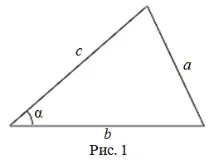
Косинусовата теорема е обобщение на Питагоровата теорема. Изявления, обобщаващи Питагоровата теорема и еквивалентни на косинусовата теорема, са формулирани поотделно за случаите на остър и тъп ъгъл в 12 и 13 изречения от II книга на Елементите от древногръцкия математик Евклид (ок. 300 г. пр. н. е.). Изявления, еквивалентни на косинусовата теорема за сферичен триъгълник, са използвани в трудовете на математиците в Централна Азия. Косинусовата теорема за сферичен триъгълник в обичайната му форма е формулирана от изключителния немски астролог, астроном и математик Региомонтанус (1436 - 1476), наричайки я "теорема на Албатегниус" (на името на изключителния средновековен астроном и математик Абу Абдала Мохамед ибн Джабир ибн Синан ал-Батани (858 - 929).
В Европа косинусовата теорема е популяризирана от френския математик Франсоа Виет (1540 - 1603) през 16 век. В началото на 19 век започва да се записва с възприетата и до днес алгебрична нотация.
Следствие от косинусовата теорема
Косинусовата теорема може да се използва за намиране на косинуса на ъгъла на триъгълник (фиг. 1):
Ако $b^+c^-a^>0$, тогава ъгълът $\alpha$ е остър;
Ако $b^+c^-a^=0$, тогава ъгълът $\alpha$ е прав ъгъл;
Задача. В триъгълник $ABC AC=3, BC=5$ и $AB = 6 .$ Намерете ъгъла срещу страната $AB$
Решение. Съгласно следствието от косинусовата теорема имаме:
$$\ъгъл A C B=\arccos\left(-\frac\right)$$
Отговор. $\angle A C B=\arccos \left(-\frac\right)$
Задача. Даден ви е триъгълник $ABC$ с дължини на страните $AC=17, BC=14, \angle ACB=60^$. Намерете дължината на третата страна на разглеждания триъгълник.
Решение. Според закона на косинусите
$$A B^=A C^+B C^-2 \cdot A C \cdot B C \cdot \cos \angle A C B=$$
$$=17^+14^-2 \cdot 17 \cdot 14 \cdot \cos 60^=289+196-238=24$$