Формула на Лагранж

Нека използваме геометричния смисъл на производната, за да дадем ясно обяснение на валидността на факта, че има допирателна към графиката f в точка с абсцисата c от интервала (a; b), успоредна на секанса, минаващ през точките A (a; f (a)), B (b; f (b)).

Да разгледаме права l, успоредна на AB и нямаща общи точки с частта от графиката, съответстваща на интервала [a; b]. Ще преместим тази права l към графиката f, така че да остане успоредна на AB. Нека фиксираме позицията l0 на тази права в момента, в който тя има общи точки с тази част от графиката.

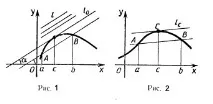
От фиг. 1 се вижда, че всяка от тези „първи“ общи точки е точката на контакт на правата l0 с графиката f. Нека означим абсцисата на тази точка чрез c. Тогава f'(c)=tg α, където α е ъгълът между правата l0 и оста x. Но lAB, така че ъгълът α е равен на ъгъла на наклона на секущата AB, т.е.

Така че, ако функцията е диференцируема, тогава на интервала (a; b) има точка c∈ (a; b) (фиг. 2), така че

Тази формула се наричаформула на Лагранж.

---