Функция y x^n линейна функция, квадратна, кубична и y 1
Степенна функция е функция от вида y=x n (чете се като y е равно на x на степен n), където n е дадено число. Частни случаи на степенни функции са функции от вида y=x, y=x 2 , y=x 3 , y=1/x и много други. Нека поговорим повече за всеки от тях.
Линейна функция y=x 1 (y=x)
Графиката е права линия, минаваща през точката (0; 0) под ъгъл от 45 градуса спрямо положителната посока на оста Ox.
Диаграмата е показана по-долу.
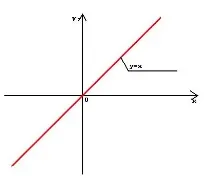
Основни свойства на линейна функция:
- Функцията е нарастваща и е дефинирана върху цялата числова ос.
- Няма максимални и минимални стойности.
Квадратична функция y=x 2
Графиката на квадратична функция е парабола.
Общият изглед на параболата е показан на фигурата по-долу.
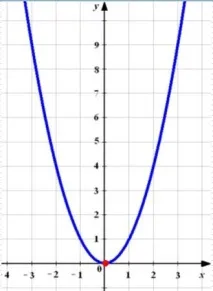
Основни свойства на квадратична функция:
- 1. За x=0, y=0 и y>0 за x0
- 2. Квадратната функция достига минималната си стойност в своя връх. Ymin при х=0; Трябва също да се отбележи, че максималната стойност на функцията не съществува.
- 3. Функцията намалява на интервала (-∞;0] и расте на интервала [0;+∞).
- 4. Противоположните x стойности съответстват на същите y стойности.
Кубична функция y=x 3
Графиката на кубична функция се нарича кубична парабола.
Общият изглед на параболата е показан на фигурата по-долу.
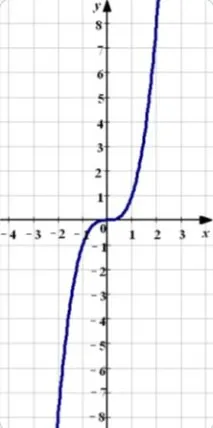
Основни свойства на кубична функция:
- 1. Когато x \u003d 0, y \u003d 0. y>0 за x>0 и y
- 2. Кубичната функция няма максимална или минимална стойност.
- 3. Кубичната функция расте по цялата реална ос (-∞;+∞).
- 4. Противоположните x стойности съответстват на противоположнотоy стойности.
Функция от вида y=x -1 (y=1/x)
Графиката на функцията y=1/x се нарича хипербола.
Общият изглед на хиперболата е показан на фигурата по-долу.