Геодезически линии
Във вътрешната геометрия на повърхността ролята на прави линии играят така наречените геодезични линии или, както се казва, просто "геодези".
Права линия в равнина може да се дефинира като линия, съставена от сегменти, частично припокриващи се един с друг. Геодезическата се дефинира по същия начин, само най-късите сегменти играят ролята на сегменти. С други думи, геодезическата линия е крива върху повърхност, така че всяка достатъчно малка дъга е най-късата дъга. Фактът, че не всяка геодезична като цяло е най-късата, може да се види на примера на повърхността на топка, където всяка дъга на голяма окръжност е геодезична, но само нейните сегменти, които не надвишават полукръговете, ще бъдат най-къси. Геодезичната може, както виждаме, дори да бъде затворена крива.
За да изясните някои важни свойства на геодезичните, разгледайте следния механичен модел. Оставете на повърхността
поставя се опъната гумена нишка с фиксирани краища (фиг. 39). Когато нишката има най-малка дължина, тя ще бъде в равновесие, тъй като всяка промяна в нейното положение е свързана с разтягане и следователно може да възникне само под въздействието на външни сили. Това означава, че нишката, разположена по най-късата линия, ще бъде в равновесие. За равновесие е необходимо еластичните сили във всяка секция на нишката да се балансират от съпротивлението на повърхността, което е насочено по нормалата към нея. (Приемаме, че повърхността е гладка и няма триене между нишката и повърхността.) Но в § 2 беше установено, че натискът, упражняван от опънатата нишка върху опората, е насочен по главната нормала към кривата, по която минава нишката. Следователно стигаме до следния резултат: главната нормала на геодезическата във всяка точка е насочена по нормалата към повърхността. Обратната теорема също е вярна: всяка крива върху правилна повърхност, която имапосочен имот, е геодезическа.
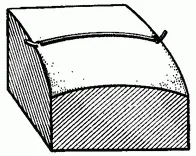
Това свойство на геодезичната линия ни позволява да открием следния забележителен факт: ако материална точка се движи по повърхността по такъв начин, че върху нея не действат никакви сили, освен реакцията на повърхността, тогава нейната траектория е геодезична. Наистина, както знаем от § 2, нормалното ускорение на точка е насочено по главната нормала към траекторията и тъй като единствената сила, действаща върху точката, е реакцията на повърхността, главната нормала към траекторията съвпада с нормалата към повърхността и по силата на последната теорема траекторията е геодезична. Последното свойство на геодезичните задълбочава още повече приликата им с правите линии. Точно както движението на свободна точка по инерция се извършва по права линия, движението на точка, принудена да остане на повърхността, в отсъствието на външни сили, се случва по геодезическа 2.
Следната теорема следва от същото свойство на геодезичните: ако две повърхности се допират една до друга по протежение на крива, която е геодезична на една от тях, тогава тази крива също ще бъде геодезична на втората повърхност. Наистина, тъй като във всяка точка на тази крива повърхностите имат обща допирателна равнина, те имат обща нормала в тези точки и тъй като кривата е геодезична на една от повърхностите, тази нормала съвпада с главната нормала към кривата. Следователно на втората повърхност кривата също ще бъде геодезична.
От този резултат следват още; две илюстративни свойства на геодезичните линии. Първо, ако еластична правоъгълна плоча (например стоманена линийка) е здраво закрепена към повърхността по нейната средна линия, тогава тя докосва тази повърхност по геодезическата линия. (Наистина, линията на контакт остава геодезическа линия на линийката иследователно се оказва геодезична и на повърхността.) Второ, ако дадена повърхност се търкаля по равнина по такъв начин, че докосва равнината по определена права линия, тогава следата от тази права линия върху повърхността е геодезична.
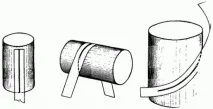
И двете свойства могат лесно да бъдат демонстрирани с помощта на примера на цилиндър и може да се провери от опит, че средната линия на плоска права лента, насложена върху цилиндъра (фиг. 40), е разположена или по протежение на образуващата, или по протежение на окръжност, или по протежение на спирала (лесно е да се докаже, че геодезичните линии върху цилиндър могат да бъдат само един от тези типове). Същите линии се отпечатват върху цилиндъра, ако го търкаляте по равнина, върху която с тебешир е начертана права линия.
Аналогията на геодезичните с линиите в равнината може да бъде допълнена с друго важно свойство, което често се приема като дефиниция на геодезичните. А именно, правите линии в равнина могат да бъдат дефинирани като криви с нулева кривина, а геодезичните линии върху повърхност могат да бъдат дефинирани като криви с нулева геодезична кривина. (Припомнете си, че геодезичната кривина е кривината на проекцията на кривата върху допирателната равнина на повърхността в точката на изследваната крива; вижте Фиг. 37.) Естественото съвпадение на това определение на геодезичните с оригиналното може да се обясни със следните съображения. Ако във всяка точка на определена линия кривината на проекцията върху допирателната равнина е равна на нула, тогава кривата се отклонява от допирателната си главно в посока на нормалата
към повърхността и следователно главната нормала на кривата винаги е насочена по нормалата към повърхността и кривата се оказва геодезична в първоначално посочения смисъл. Напротив, ако кривата е геодезична, тогава нейната основна норма и следователно основната част от отклонението от допирателната на правата линия е насочена към нормалата към повърхността, следователно, когато се проектира върхудопирателна равнина се получава крива, при която отклонението от допирателната е значително по-малко от това на оригиналната крива, а кривината на получената проекция се оказва нулева.
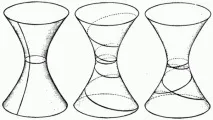
Ходът на геодезиката върху различни повърхности може да бъде много разнообразен. За пример на фиг. 41 показва няколко геодезически върху хиперболоид на революция.