Характеристики на случайните сигнали
Тъй като всички информационни сигнали и смущения са случайни и могат да бъдат предвидени само с определена степен на вероятност, теорията на вероятностите се използва за описание на такива сигнали. В този случай се използват статистически характеристики, които се получават чрез провеждане на множество експерименти при едни и същи условия.
Всички случайни явления, изучавани от теорията на вероятностите, могат да бъдат разделени на три групи: - случайни събития; —случайни променливи; - произволни процеси.
Случайно събитие е всеки факт, който в резултат на опит може да се случи или да не се случи. Случайно събитие е поява на смущение на входа на приемника или получаване на съобщение с грешка. Случайните събития се обозначават с латински букви A, B, C.
Числените характеристики на случайно събитие са: 1. Честота на възникване на случайно събитие:
където m е броят на експериментите, в които се е случило това събитие; N е общият брой извършени експерименти.
Както следва от израз (40), честотата на възникване на случайно събитие не може да надвишава 1, тъй като броят на експериментите, в които се е случило това събитие, не може да надвишава общия брой експерименти. 2. Вероятност за възникване на случайно събитие:
Тоест, вероятността за възникване на случайно събитие е честотата на неговото възникване с неограничено увеличение на броя на извършените експерименти. Вероятността за настъпване на събитие не може да надвишава 1. Случайно събитие с вероятност, равна на единица, е надеждно, т.е. определено ще се случи, следователно събитията, които вече са се случили, имат такава вероятност. Случайната стойност е стойност, която се променя произволно от опит на опит. Случайната променлива е амплитудата на шума на входа на приемника или броя на грешките вполучено съобщение. Случайните променливи се означават с латински букви X, Y, Z, а техните стойности са x, y, z. Случайните променливи са дискретни и непрекъснати. Дискретната променлива е случайна променлива, която може да приема краен набор от стойности (например количество оборудване, брой телеграми и т.н., тъй като те могат да приемат само цяло число 1, 2, 3, ...). Непрекъснатата е случайна променлива, която може да приема всякакви стойности от определен диапазон (например амплитудата на шума на входа на приемника може да приема всякакви стойности, точно както информационен аналогов сигнал може да приема всякакви стойности).
Числените, статистически характеристики, описващи случайни променливи са: 1.Функция на разпределение на вероятността.
Тази функция показва вероятността случайна променлива X да не надхвърли определена стойност на x. Ако случайната променлива X е дискретна, тогава F(x) също е дискретна функция, ако X е непрекъсната стойност, тогава F(x) ? непрекъсната функция. 2.Плътност на вероятността.
Тази характеристика показва вероятността стойността на случайна променлива да попадне в малък интервал dx в близост до точката x', т.е. в защрихованата област (фигура).
3.Математическо очакване.
където xi са стойностите на случайна променлива; Р(хi) е вероятността за поява на тези стойности; n е броят на възможните стойности на случайната променлива.
където p(x) е плътността на вероятността на непрекъсната случайна променлива.
По смисъла си математическото очакване показва средната и най-вероятната стойност на случайна променлива, т.е. тази стойност най-често се приема от случайна променлива. Израз (44) се прилага, ако случайната променливае дискретна, а израз (45), ако е непрекъсната. Нотацията M[X] е специална за математическото очакване на случайната променлива, дадена в квадратни скоби, но понякога се използва нотацията mх или m.
4.Дисперсия.
Дисперсията характеризира количествено степента на разсейване на резултатите от отделните експерименти спрямо средната стойност. Нотацията за дисперсията на случайна променлива D[X] е общоприета, но нотацията ??x също може да се използва. Израз (46) се използва за изчисляване на дисперсията на дискретна случайна променлива, а (47) се използва за изчисляване на дисперсията на непрекъсната случайна променлива. Ако вземете корен квадратен от дисперсията, ще получите стойност, наречена стандартно отклонение (?x).
Всички характеристики на случайна променлива могат да бъдат показани с помощта на фигура 22.
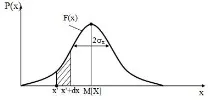
Фигура 22 - Характеристики на случайна променлива
Случайният процес е функция на времето t, чиято стойност за всяка фиксирана времева стойност е случайна променлива. Например, фигура 23 показва диаграма на някакъв случаен процес, наблюдаван в резултат на три експеримента. Ако определим стойността на функциите във фиксирано време t1, тогава получените стойности ще се окажат случайни променливи.
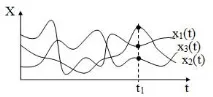
Фигура 23 - Ансамбъл от реализации на случаен процес
За характеризиране на случайни процеси се използват същите характеристики като за случайните променливи: функция на разпределение на вероятностите, плътност на разпределение на вероятностите, математическо очакване и дисперсия. Тези характеристики се изчисляват по същия начин, както при случайните променливи. Случайните процеси са от различни видове. В телекомуникациите обаче повечето случайни сигналии шумът са свързани със стационарни ергодични случайни процеси.
Стационарен е случаен процес, чиито характеристики F(x), P(x), M[X] и D[X] не зависят от времето.Ергодичният е процес, при който усредняването на времето на една от реализациите води до същите резултати като статичното осредняване на всички реализации. Физически това означава, че всички реализации на ергодичния процес са подобни една на друга, така че измерванията и изчисленията на характеристиките на такъв процес могат да се извършват с помощта на една (която и да е) от реализациите. В допълнение към четирите характеристики на горното, случайните процеси също се описват от корелационната функция и спектралната плътност на мощността.
Корелационната функция характеризира степента на връзка между стойностите на случаен процес в различни времена t и t+?. Където ? изместване на времето.
където tн е времето за наблюдение на реализацията xk(t).
Спектрална плътност на мощността - показва разпределението на мощността на произволен процес по честоти.
където ?Р е мощността на случайния процес за честотна лента ?f.
По този начин наблюдението на случайно явление във времето е случаен процес, появата му е случайно събитие, а стойността му е случайна величина.
Например, наблюдението на телеграфен сигнал на изхода на комуникационната линия за известно време е случаен процес, появата на неговия дискретен елемент „1“ или „0“ при приемане е случайно събитие, а амплитудата на този елемент е случайна стойност.