Хармоничен анализ
Както може да се види от фигурата, с цифровия метод за измерване и съхраняване на данни част от оригиналната информация ще бъде загубена. За да се подобри точността на измерванията, е необходимо да се увеличи битовата дълбочина и честотата на семплиране на техниката на преобразуване.
Да се върнем към поставената задача - да определим наличието на определена честота в произволен сигнал. За по-голяма яснота на използваните техники, разгледайте сигнал, който е сумата от две хармонични трептения:q=sin2t+sin5t, дадени с дискретностΔt=0.2(фиг. 19). Таблицата на фигурата показва стойностите на получената функция, която по-нататък ще разгледаме като пример за някакъв произволен сигнал.
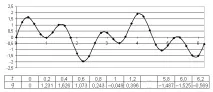
За да проверим наличието на честотата, която ни интересува в изследвания сигнал, ние умножаваме оригиналната функция по зависимостта на промяната на осцилаторната стойност при проверяваната честота. След това добавяме (числово интегрираме) получената функция. Ще умножаваме и сумираме сигналите на определен интервал - периода на носещата (основната) честота. При избора на стойността на основната честота трябва да се има предвид, че е възможно да се провери само честота, която еnпъти по-голяма от основната. Да изберем като основна честотаω=1, която съответства на периода.
(10)
Нека започнем проверката веднага с "правилната" (присъстваща в сигнала) честотаyn=sin2x. На фиг. 20 описаните по-горе действия са представени графично и числено. Обърнете внимание, че резултатът от умножението е предимно над оста x и следователно сборът е забележимо по-голям от нула (15,704>0). Подобен резултат ще бъде получен чрез умножаване на оригиналния сигнал поqn=sin5t(петият хармоник също присъства в сигнала, който се изследва). Ирезултатът от изчисляването на сумата ще бъде толкова по-голям, колкото по-голяма е амплитудата на тествания сигнал в теста.