Хармонични индукционни процеси
В предишния раздел разгледахме работата на генераторите за постоянен ток и участието на сили на трети страни в процеса на генериране на електроенергия. Основният извод от това разглеждане е, че процесът на генериране на електрическа енергия не трябва да се бърка с процесите на нейното превръщане в други видове енергия (работа, топлина и др.). Това е същата грешка, допусната от няколко видни изследователи. За съжаление, много специалисти по електродинамика все още се спъват в един и същи камък, което значително изкривява нашето разбиране за електромагнитните взаимодействия.
Генератор на хармонична индукция
Електромагнитната индукция е процес на преобразуване на различни видове енергия (предимно механична) в електрическа енергия. Всички генератори на променлив ток работят на този принцип - от велосипеден "динамит" до най-мощните агрегати във водноелектрическите централи. Принципът на генериране на електричество с помощта на електромагнитна индукция е същият като при други (например химически) електрически генератори: противодействайки на силите на Кулон, силите на трети страни пренасят електрически заряди към изходните полюси на генератора, като по този начин създават потенциална разлика - потенциална електрическа енергия.
Външните сили в индукционните генератори са "магнитни сили". Според Фарадей, в проводник, пресичащ линиите на магнитното поле, магнитните сили създават поток от електрони. Този ток естраничен ток, който създава потенциална разлика в краищата на проводника - ЕМП. Нека се съгласим да наричаме "индуктивен ток" само този - ток на трета страна. Според Фарадей индукционният токпредшествапоявата на индукционната ЕМП. Днес бихме казали, че индукционният токводииндукционната ЕМП във фаза.
През първата половина на 19 век електродинамикатаусвоени постоянни токове. Нямаше идеи за хармонични токове, фазови измествания и т.н. Правилата за разклонени постоянни вериги бяха формулирани от Кирхоф едва през 1847 г. При верига със синусоидални токове тези правила са D.U. Rayleigh разпространява едва през 1886г.
През 20-ти век електротехниката преминава главно към производството и използването на променливи токове. Електричеството се генерира от индукционни генератори, които създаватхармоничниЕМП. Но подробен анализ на работата на ЕМП в процесите на генериране на хармонични токове липсва. Основните принципи и концепции на електромагнитната индукция, разбира се, останаха същите като при Фарадей и Максуел. Но това явление е обогатено с нови параметри, разглеждането на които може да разкрие някои интересни характеристики на индукционния процес.
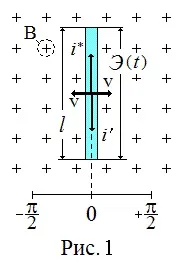
За да получим хармонична ЕМП в движещ се проводник с дължинаl(виж Фиг. 1), ние ще принудим проводящия сегмент да извършва осцилаторни движения в еднообразно магнитно поле с индукцияBс промяна на скоростта, например, съгласно закона
| (1) |
където vm е амплитудата иωе цикличната честота на трептене.
Елементарният магнитен поток, който преминава през проводника за времетоdtсе определя от зависимостта
| (2) |
Интегрирането на този израз дава хармоничната функция за магнитния поток, преминаващ от проводника:
| (3) |
където е амплитудната стойност на магнитния поток.
В това съображение третата („магнитна“) сила по големина и посока може да бъде представена чрез формулата на Лоренц, според която силата е пропорционална на скоростта на пресичане на линиите на магнитното поле с електрически заряди (скоростта на проводника) и следователно се описва от хармонична функция, която е във фаза със скоростта (1):
| (4) |
Тук е стойността на амплитудата на външната сила.
Магнитната сила създава хармоничен индукционен ток в проводника
| (5) |
което може да се представи като съотношение за елементарния заряд
| (6) |
Интегрирайки (6), получаваме зависимостта от времето на количеството заряд, създаден в краищата на проводника от външен ток,
| (7) |
къде е максималното зареждане. Зарядите, натрупани в краищата на проводника, създават индуктивна ЕМПE(t), пропорционална на заряда. Следователно зависимостта на индукционната едс от времето ще бъде изразена с подобна функция
| (8) |
който съвпада по фаза с магнитния поток, но една четвърт от периодаизоставаот външния ток (5).
Фазовото изместване между генерираната ЕМП и индукционния ток ехарактерна чертана индукционния процес - „визитна картичка“ на външни сили!
Едновременно с индукционната ЕМП в такъв микрогенератор възниква и обратна ЕМП
| (9) |
През втората четвърт на периода, когато силата на Лоренц променя посоката си, под действието на товаEMF в проводника се появява обратен (потенциал, "Coulomb") ток
| (10) |
Эiизоставащ от ЕМП с една четвърт от периода исъвпадащ във фазас външен ток (5). Имайте предвид, чеi'не е "чисто" потенциален ток. Въпреки че се създава от потенциалния ЕМПEi, във формирането му участва и външна сила. Това е причината за фазовото изоставане на този ток от обратната ЕМП.
До края на втората четвърт от периода проводникът е напълно "разреден", двете ЕМП (EиEi) се превръщат в нула и токът става чисто външен.
Така през първата и третата четвърт на периода се генерира електрическа енергия, а през втората и четвъртата тя се разсейва в джаулова топлина.
На фиг. 2,азависимостите (1)-(5) и (8)-(10) са показани в координатна форма, а на фиг. 2,b- векторна диаграма, която показва фазовите отношения между електрическите параметри в отворен "микрогенератор":
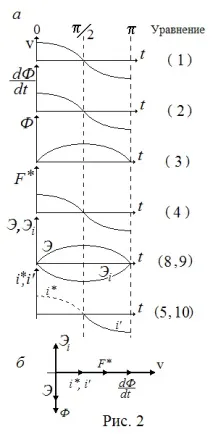
Ако микрогенераторът е свързан към външно съпротивлениеR, тогава индукционният ЕМП (8) ще създадевъв външната веригавъв фаза с негопотенциалток
| (единадесет) |
къдетоim =Em/Rе неговата амплитудна стойност. Вижда се, че този токне съвпадапо фаза с външния ток (5) иизоставаот него с една четвърт от периода. В краищата на проводника електрическият ток претърпява "прекъсване".
Имайте предвид, че в "затворен" режим ЕМП, генериран от външна сила, се "разрежда" в двете посоки - както към външната верига, така и "вътре" в генератора (с обратен ток). Следователно индукционната ЕМПEсе променя с времето по закон, различен от хармоничния, и не достига стойността (8), както в режим на работа "на празен ход". Съответно всичкитокове губят своя хармоничен характер. Всички индустриални индукционни електрогенератори работят в този режим - затворен към външен товар. Но във вериги на генератор с висока мощност, тази анхармоничност на ЕМП не се забелязва.
Фазови връзки в затворен цикъл
Електромагнитната индукция в затворена проводяща верига е може би единственият пример, при който генерирането и разсейването на електрическа енергия се случват едновременно. Но хармоничният режим тук има своите особености.
Индукционният ток винаги има такава посока, че отслабва действието на причината, която възбужда този ток.
Токът е насочен така, че механичната сила, действаща върху движещия се проводник, е противоположна на скоростта (забавя движението).
Обсъждайки появата на индуктивна ЕМП в затворена верига, използвайки метода на пресичане, ние показахме, че тази верига може да бъде сглобена отnмикрогенератори с отворен контурчрез ограничаване наn→ ∞. От това следва, че в затворена верига трябва да се спазват същите фазови съотношения, както и в отворен микрогенератор, тоест външният ток трябва да съвпада по фаза собратния(потенциален) ток и с производнатаdФ/dt(виж фиг. 2,b). Това означава, че знакът "+" трябва да е в закона на Максуел. Всичко обаче не е толкова просто - контуръте затворен! И в затворен микрогенератор има едновременно потенциални токове както в посоката на индукционната ЕМП (прав ток), така и в обратна посока (обратен ток). Какви фазови отношения са изпълнени в хармоничен индукционен процес взатворенпръстен?
Затворената индукционна верига се различава от микрогенератора, затворен за натоварване, тъй като "външната" верига не се различава от "вътрешната" - ЕМП се генериравъв всичкоконтур. Следователно потенциалният ток в затворена верига, както и в отворен микрогенератор, епродължениена външен ток (виж фиг. 2,aa). Няма прекъсване на тока, както е при микрогенератор, натоварен с активен товар. Тоест, в затворена индукционна верига всички фазови отношения, характерни за отворен микрогенератор, наистина са изпълнени. В индукционен генератор ЕМП трябва да изпревари потенциалния ток, който създава. Но тогава, както се вижда от векторната диаграма на фиг. 2,b, потенциалният ток във веригата не трябва да се създава от директен, а отобратенЕМП! За това обаче е необходимо взатворенияпроводник да има "нееднородности", върху които се събират заряди, които създават обратно ЕМП. Може да се приеме, че тези нееднородности се дължат на периодичността на електричното поле в кристалната структура на проводника. Това предположение обаче изисква теоретичен анализ и допълнителни експерименти.
Друг вариант ни се струва по-правдоподобен:
В затворена верига потенциалният ЕМП ... изобщо не се появява.външната енергияпреминава директно в топлина. В полза на този вариант на електромагнитна индукция в затворенаметалнаверига могат да се дадат две съображения:
-
л). Независимо от какви сили (външни или потенциални) се движат електроните в метален проводник, механизмът на загуба на топлина е един и същ. Няма разлика в съпротивленията "напред" и "назад", както е при галваничните клетки. Това означава, че загубите на външна енергия в определен участък от проводника са същите, каквито биха били при същия потенциален ток. Това обяснява липсата на потенциална разлика във всяка част от веригата (равенствоε = Irвъв всяка частсегмент със съпротивлениеr). 2). Само такъв механизъм може да обясни тозиспециален случай, когато индуцираната ЕДС остава постоянна за известно време.
Във всеки случай по-нататъшният анализ на процеса на индукция в затворена проводяща верига е само от академичен интерес. Реалните електрически генератори работят, като правило, в режим на индукционен генератор, затворен за външен товар.
| [1] | Sivukhin DVОбщ курс по физика. Т. 3. Електричество. Москва: Физматлит, 2004, стр. 260. |
| [2] | Калашников С.К.Електричество. Москва: Физматлит, 2004, стр. 197. |