Интерполация по схемата на Айткен - Студиопедия
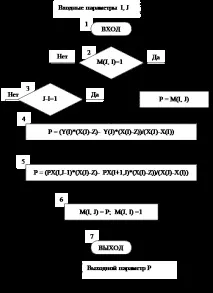
Итеративните интерполационни методи се основават на многократното прилагане на някаква проста интерполационна схема. Най-известният от итеративните методи е методът на Aitken, който се основава на многократно прилагане на линейна интерполация.
Когато се интерполира върху три или повече точки, полиномите се изчисляват последователно
Основното предимство на схемата на Aitken е възможността за постепенно увеличаване на броя на използванитеxiстойности, докато последователните стойностиP0,1,2,…,n(x) иP1,2,…,n-1(x) съвпадат в определената точност . С други думи, изчисленията спират, когато условието
P0,1,2,…,n(x) -P1,2,…,n-1(x) I), посочете дали съответнитеP(x) стойности са били изчислени досега и се определят като
1.3. Интерполационни формули на Нютон
за еднакво разположени възли
Интерполационни възлиx0,x1, .xnсе наричат равноотдалечени, ако , къдетоhе стъпката на интерполация. В този случай, за някаква функцияf(x), стойноститеyi = f(xi), къдетоxi = x0+ ih, са дадени в таблица.
Има две формули на Нютон за случая на равноотдалечени възли на интерполация, които се наричат съответно първа и втора формула на интерполация на Нютон и имат формата:
;
,
В тези формули Di yjса крайните разлики, къдетоiе редът на разликата,jе нейният пореден номер, а параметритеtиqсе дефинират както следва:
Крайните разлики от първи ред се изчисляват като Dyj=yj+1 –yj, къдетоj=, за по-високи порядъци се използва добре известната формула
(i= 2, 3, . ;j= ).
Удобно е да се представят получените окончателни разлики в таблична форма, например под формата на таблица. 1, която се нарича хоризонтална таблица с крайни разлики.
Таблица 1
| x | y | Dy | D2y | D3y | D4y |
| x0 | Y0 | Dy0 | D2y0 | D3y0 | D4y0 |
| x1 | Y1 | Dy1 | D2y1 | D3y1 | D4y1 |
| x2 | Y2 | Dy2 | D2y2 | D3y2 | -[s1] |
| x3 | Y3 | Dy3 | D2y3 | - | -[s2] |
| x4 | Y4 | Dy4 | - | - | -[s3] |
| x5 | Y5 | - | - | - | -[s4] |
Първата формула на Нютон се използва за интерполация напред и екстраполация назад, т.е. в началото на таблицата на разликите, където редовете са попълнени и има достатъчен брой крайни разлики. Когато използвате тази формула за интерполация, стойността на аргументаxтрябва да лежи в интервала [x0,x1]. В този случайx0 може да се приеме като всеки интерполационен възелxkс индекс, къдетоmе максималният ред на крайните разлики.
Втората формула на Нютон се използва за обратна интерполация и екстраполация напред, т.е. в края на таблицата с крайни разлики. В този случай стойността на аргументаxтрябва да бъде в интервала [xn-1,xn] и всеки възел на интерполация може да се приеме катоxn.
Едно от най-важните свойства на крайните разлики е следното. Ако крайните разликиiти ред (i
Не намерихте това, което търсихте? Използвайте търсачката:
Деактивирайте adBlock! и обновете страницата (F5)наистина е необходимо