Историята на изграждането на музикалната гама
„Мислейки за изкуството и науката, за техните взаимни връзки и противоречия, стигнах до извода, че математиката и музиката са на крайните полюси на човешкия дух, че тези два антипода са ограничени и обусловени от цялата творческа духовна дейност на човека и че всичко, което човечеството е създало в областта на науката и изкуството, се намира между тях.“
G. Neuhaus
Аз. Историческа бележка
1. Откритие на Питагор в областта на музикалната теория.
Същността му е, че комбинацията от звуци, издавани от струните, е най-хармонична, ако дължините на струните на музикалния инструмент са в правилно цифрово съотношение една спрямо друга.
За да осъществи откритието си, Питагор използвамонокорд- полуинструмент, полуустройство. Под струната на горния капак ученият нарисува скала, с която е възможно да се раздели струната на части. Проведени са много експерименти, в резултат на които Питагор описва математически звука на опъната струна.
2. Какво определя съзвучието.
Дълго време нямаше консенсус относно това какво определя звука на една струна, който е приятен за ухото (в музиката това явление се наричаконсонанс). Този въпрос е изяснен от Архит (4 век пр. н. е.), който вижда същността на тона не в дължината на струната и не в силата на опън, а в скоростта на нейното движение, т.е. скорост на въздействие на струната върху частиците на въздуха.
Днес тази "скорост на движение" се наричачестота на вибрацияна струната. Архит открива, че височината (или честотата на струната) е обратно пропорционална на нейната дължина.
3. Закони на питагорейската музика.
Тази музикална система се основава на два закона, които носят имената на двама велики учени - Питагор и Архит. Това са законите:
1. Две звучащи струни определят съзвучието, ако дължините им са съотнесени като цели числа, образуващи триъгълно число 10=1+2+3+4, т.е. като 1:2, 2:3, 3:4. Освен това, колкото по-малко е числото n по отношение наn:(n+1)(n=1,2,3), толкова по-консонантен е полученият интервал.
2. Честотата на трептенеwна звучаща струна е обратно пропорционална на нейната дължинаl.
къдетоaе коефициентът, характеризиращ физическите свойства на струната.
II. Някои концепции на музикалната теория
1. Гама, илискал, е поредица от звуци, подредени отосновен тон(звук) във възходящ или низходящ ред.
2. Интервалътмежду тоновете е поредният номер на степента на горния тон спрямо долния в дадената гама.
Интервалъткоефициентътна два тона е отношението на честотата на трептене на горния тон към честотата на трептене на долния:
Някои интервални коефициенти и съответните им интервали през Средновековието са били наричанисъвършени съзвучияи са получили следните имена:
3. Тоника- основният най-устойчив тон в гамата. Тази музикална система започва с него.
Рамка- приятна връзка на музикални звуци, определена от зависимостта на нестабилни звуци от стабилни и имащи определен звуков характер.
Музикална гама –математически израз на системата от съотношения на височината – праг.
III. Математическо описание на конструкцията на музикална гама
1. В основата на музикалната гама-гама на питагорейците е бил интервалът -октава. Това е съзвучие, което повтаря горния звук. За да изградят музикална гама, питагорейците трябваше да разделят октаватана добре звучащи части. Тъй като вярваха в идеалните пропорции, те свързаха устройството на скалата със средни стойности:аритметика, хармоника.
Средноаритметичнотона честотите на вибрациите на тониката (w1) и нейното повторение в октавата (w2) помага да се намери идеалното съзвучиеквинта.
Дължината на струнатаl3, съответстваща на петата, според втория закон на Питагор-Архит, ще бъдесредно хармоничноот дължините на струните на тоникатаl1и нейното октавно повторениеl2.
Така чеw4:w1= 4 : 3. В резултат на това намираме още едно съвършено съзвучие -четвърто.
Нека определим как са свързани дължините на низовете на намерените честоти (l4иl1):
Това означава, че дължините на низоветеl1,l2иl4са свързани помежду си чрез средно аритметично.
И така,честотата на трептенепетиесредно аритметичнона основнитеw1и октавнитеw2честоти, а честотата начетвъртиесредно хармоничноw1иw2. Или с други думи:дължината на петата струнаесредно хармоничнона дължината на струнатаl1и октаватаl2, адължината на струната на четвъртияесредно аритметичноl1иl2. Това е само малка част от тези прекрасни пропорции, които бяха въплътени в музикалната гама на Питагор.
2. Древните гърци са имали и друг начин за конструиране на музикална гама, в допълнение към описания по-горе. Беше по-просто и удобно и все още се използва при настройка на музикални инструменти.
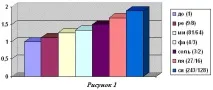
Оказва се, че гамата може да се изгради само с перфектни съзвучия - квинта и октава. Същността на този метод е, че от изходящия звук, например "до" (3/2) 0 = 1, се движим нагоре и надолу в четвърти иполучените звуци се събират в една октава. И тогава получаваме: (3/2) 1 = 3/2 - сол, (3/2) 2: 2 = 9/8 - re, (3/2) 3: 2 = 27/16 - la, (3/2) 4: 22 = 81/64 - mi, (3/2) 5: 22 = 243/128 - si, (3/2) -1: 2 = 4/3 - фаза. (Всички математически изчисления се извършват на компютър с помощта на програмата Calculator.)
Нека използваме възможностите на компютъра, по-точно текстообработващата програма MS Word:
| преди (1) | 1 |
| повторно (9/8) | 1.125 |
| мили (81/64) | 1,266 |
| fa (4/3) | 1,333 |
| сол (3/2) | 1.5 |
| ла (27/16) | 1,687 |
| си (243/128) | 1,898 |
За по-голяма яснота изграждаме съответната диаграма на музикалната гама:
Или като графика:
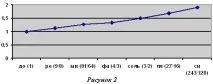
Подреждайки тези звуци в ред, получавамеПитагоровата система на лидийската гама. Въз основа на възможните конструкции на гамата са получени няколко наименования на тетракорда - четиристепенна гама в рамките на четвъртата. Това са дорийската, фригийската и вече споменатата лидийска система на музикалната гама.
Последната конструкция на музикалната скала има следната характеристика: движейки се нагоре и надолу в пети, няма да получите точно повторение на октавата на оригиналния звук. Само 12 пети са приблизително равни на 7 октави, а интервалът, който ги разделя, се наричаПитагорова запетая. Въпреки своята дребност, питагорейската запетая от векове "реже ухото" на музикантите. Като вземете съотношението (3/2) 12:27 (с помощта на калкулатор), можете да намерите числената стойност на питагоровата запетая (1,0136).
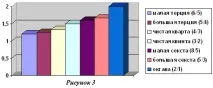
3. Идеята за съвършенството на околния свят доминираше в умовете на учените през следващите епохи. През първата половина на XVII век. I. Kepler установи седемосновни хармоникаинтервали: октава - 2/1, голяма секста - 5/3, малка секста - 8/5, перфектна квинта - 3/2, перфектна кварта - 4/3, голяма терца - 5/4 и малка терца - 6/5.
малка терца (6/5)
голяма терца (5/4)
чист литър (4/3)
перфектна пета (3/2)
малка шеста (8/5)
голяма шеста (5/3)
октава (2/1)
Нека да разгледаме съответната диаграма:
Или с графика:
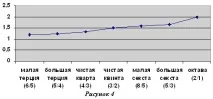
С помощта на тези интервали той показва цялата гама от мажорни и минорни настроения. След дълго търсене на хармонични отношения "в небето", след като извърши много изчислителна работа, И. Кеплер установи, че съотношенията на екстремните ъгли на скоростта за някои планети са близки до хармоничните: Марс - 3/2, Юпитер - 6/5, Сатурн - 5/4. „Слънцето на хармонията грееше в целия си блясък. Небесното движение не е нищо друго освен музика, която не спира нито за миг“, смята ученият. Тук Кеплер не оставя бурна фантазия. Той обяснява леките несъответствия в изчисленията и наблюденията с факта, че небесният секстет трябва да звучи по един и същи начин както в мажор, така и в минор, а за това трябва да може да преустрои инструментите си.
Освен това Кеплер пише, че Сатурн и Юпитер "пеят" в бас, а Марс - в тенор, Земята и Венера - в алт, а Меркурий - в дискант. Той не предоставя никакви доказателства. Извършвайки множество изчисления, ученият беше уморен в търсене на универсална хармония. „Мозъкът ми се изморява, когато се опитвам да разбера какво съм написал и вече ми е трудно да възстановя връзката между рисунките и текста, която сам някога съм намерил“, пише известният астроном и математик. В естествознанието идва ново време: търсенията на И. Кеплер са заменени от откритията на Нютон.
Първо беше дадено физическото определение на звука. музикален тон,както вече споменахме, има колебателен процес с някаква фиксирана честота. Известно е, че човешкото ухо е в състояние да възприема честотни колебания от 16 до 20 000 Hz.
В основата на устройството на музикалната гама са определени модели. За да се изгради гама, се оказва много по-удобно да се използватлогаритмина съответните честоти: log 2w0, log 2w1. дневник 2wm. Октава (w0,2w0) в този случай ще влезе в интервала от log 2w0до log 2w0= log 2w0+1, т.е. в интервал с дължина 1. Геометрична прогресияw0, w1. wmще съответства на аритметичния дневник 2w0, дневник 2w1,…, дневник 2wm. Така по логаритмичната ос скалата ще се състои от точки A, A+1/m; А+2/м;. ; A+1, където A е стойност. На колко части трябва да се раздели музикалната гама, на какво е равно m? Анализът на много традиционни образци на народната музика показа, че най-често тя съдържа интервали, изразени с честотни съотношения: 2 (октава), 3/2 (пета), 5/4 (терца), 4/3 (четвърта), 5/3 (шеста), 9/8 (втора), 15/8 (септим). Тези и други открития показват, че музикалната гама трябва да бъде разделена на 12 части. Съотношението на съседните честоти с еднакъв темперамент е постоянно и равно.