Изчисляване на координати на точки от отворен линейно-ъглов ход
Всяка определена точка от линейно-ъгловия ход има две координати X и Y, които са неизвестни и трябва да бъдат намерени. Общият брой на точките в курса ще бъде означен с n, тогава броят на неизвестните ще бъде 2 * ( n - 2 ), тъй като координатите на две точки (първоначално начало и край) са известни. За да намерите 2 * ( n - 2 ) неизвестни, е достатъчно да извършите 2 * ( n - 2 ) измервания.
Нека изчислим колко измервания се извършват в отворен линейно-ъглов ход: n ъгли се измерват в n точки - по един във всяка точка, също се измерват ( n - 1 ) страни на курса, общо се оказва ( 2 * n - 1 ) измервания (фиг. 2.18).
Разликата между броя на направените измервания и броя на необходимите измервания е:
(2,65)
т.е. три измерения са излишни: ъгълът в предпоследната точка на хода, ъгълът в последната точка на хода и последната страна на хода. Но въпреки това тези измервания се правят и те трябва да се използват при изчисляване на координатите на точките на движение.
В геодезическите конструкции всяко излишно измерване генерира някакво условие, така че броят на условията е равен на броя на излишните измервания; при отворен линейно-ъглов ход трябва да бъдат изпълнени три условия: условието за дирекционни ъгли и две координатни условия.
Състояние на дирекционните ъгли. Изчисляваме последователно дирекционните ъгли на всички страни на хода, като използваме формулата за прехвърляне на дирекционния ъгъл към следващата страна на хода:
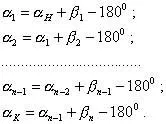
Нека добавим тези равенства и получаваме:
откъдето и (2.67)
Това е математическа нотация на първото геометрично условие в отворен линейно-ъглов ход. За прави ъгли на въртене ще бъде записано, както следва:
(2,68)
Сумата от ъглите, изчислена по формулите (2.67) и (2.68), се наричатеоретична сума от ъгли на ход. Сумата от измерените ъгли поради грешки в измерването, като правило, се различава от теоретичната сума с известна сума, наречена ъглово несъответствие и обозначена с fβ:
(2,69)
Допустимата стойност на ъгловото несъответствие може да се разглежда като пределната грешка на сумата от измерените ъгли:
(2,70)
Използваме добре познатата формула от теорията на грешките, за да намерим средната квадратична грешка на функция като сума от аргументи (раздел 1.11.2):
(2,71)
С получаваме или (2.72)
След като заместим (2.72) в (2.70), получаваме:
(2,73)
За теодолитни траверси mβ = 30", следователно:
(2,74)
Един от етапите на настройка е въвеждането на корекции на измерените стойности, за да се приведат в съответствие с геометричните условия. Нека означим корекцията към измерения ъгъл Vβ и запишем условието:
откъдето следва, че:
(2,75)
т.е. корекциите на ъглите трябва да бъдат избрани така, че тяхната сума да е равна на ъгловото несъответствие с обратен знак.
В уравнение (2.75) има n неизвестни и за решаването му е необходимо да се наложат допълнителни условия върху корекциите Vβ (n-1); Най-простата версия на тези условия би била:
(2,76)
т.е. всички корекции на измерените ъгли са еднакви. В този случай решението на уравнение (2.75) се получава във формата:
(2,77)
това означава, че ъгловото несъответствие fβ се разпределя с обратен знак еднакво за всички измерени ъгли.
Коригираните стойности на ъгъла се изчисляват по формулата:
(2,78)
Според коригираните ъгли на завъртане се изчисляват дирекционните ъгли на всички страни на трасето; съвпадението на изчислените и зададените стойности на крайния начален насочен ъгъл е контролът на правилността на обработката на ъглови измервания.
координатни условия. Решавайки последователно директния геодезичен проблем, ние изчисляваме увеличенията на координатите по протежение на всяка страна на хода ΔXi и ΔYi. Координатите на точките на движение ще бъдат получени по формулите:
(2,79)
Събираме тези равенства и получаваме за увеличенията ΔXi:
След като донесем подобни, имаме:
или
(2,80)
Подобна формула за сумата от увеличения ΔY е:
(2,81)
Получихме още две условия (2.80) и (2.81), които се наричат координатни условия. Сумите на нарастванията на координатите, изчислени по тези формули, се наричат теоретични суми на нарастванията. Поради грешките на измерване на страните и опростения метод за разпределение на ъгловия остатък, сумите на изчислените увеличения на координатите в общия случай няма да бъдат равни на теоретичните суми; има така наречените координатни остатъци на курса:
(2,82)
които изчисляват абсолютното несъответствие на курса:
(2,83)
и след това относителния остатък от хода:
(2,84)
Регулирането на нарастванията ΔX и ΔY се извършва по следния начин.
Първо запишете сумите на коригираните увеличения:
и ги приравнете към теоретичните суми:
откъдето следва, че:
(2,85)
В тези уравнения за ( n - 1 ) неизвестни и за тяхното решаване е необходимо да се наложат допълнителни условия върху корекциите VX и VY. На практика корекциите на стъпките на координатите се изчисляват по формулите:
(2,91)
които съответстват на условието "корекциите на нарастванията на координатите са пропорционални на дължините на страните".
Разгледаният метод за обработка на измервания в линейно-ъглов ход може да се нарече метод на последователно разпределение на остатъците; стриктно регулиране на линейно-ъгловия ход се извършва по метода на най-малките квадрати.
След регулиране на единичен линейно-ъглов ходгрешките в позицията на неговите параграфи не са еднакви; те нарастват от началото и края на хода до средата му, като точката в средата на хода има най-голяма грешка в позицията. В случай на приблизителна настройка, тази грешка се оценява на половината от абсолютното несъответствие на хода fs. При стриктна настройка на траверса се извършва пълна оценка на точността, т.е. изчисляват се грешки в позицията на всяка точка на траверса, грешки в ъглите на посоката на всички страни на траверса, както и грешки в коригираните стойности на ъглите и страните на траверса.