Изчисляване на вероятности с помощта на комбинаторни формули
Вероятността за събитиеAе равна на съотношението на броя на резултатите от тестаm, в които събитиетоAможе да се появи, към общия бройnна всички елементарни резултати от теста, които образуват пълна група:
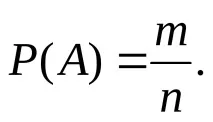
ПРИМЕР 2.1.Буквите T, E, I, Z, R, O са написани на отделни карти. Детето взема картите в произволен ред и ги поставя една върху друга. Каква е вероятността да се получат думите: а) "tor"; б) "теория"?
РЕШЕНИЕ. а) Нека събитиетоAе получаването на думата "tor". Елементарният резултат от теста е извличането на три карти от шест. Общият брой на резултатите от всички тестове е равен на броя на поставянията от 6 до 3, тъй като различните проби могат да се различават както по състав, така и по ред:
n=
Думата "tor" може да бъде получена само по един начинm=1. Тогава:
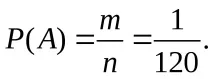
б) Нека събитиетоBе получаването на думата "теория". Елементарният резултат от теста е да се получат различни комбинации от шест букви. Общият брой на всички резултати от теста е равен на броя на пермутациите от 6, тъй като различните проби могат да се различават една от друга само по реда:
n=
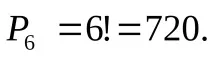
Думата "теория" може да се получи само по един начинm=1. Тогава:
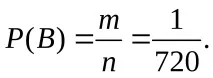
ПРИМЕР 2.2.Буквата "а" е изписана на три карти, буквата "н" - на две карти, буквата "в" - на една карта. Детето взема картите в произволен ред и ги поставя една върху друга. Каква е вероятността да получите думата "ананас"?
РЕШЕНИЕ. Нека събитиетоAе получаването на думата "ананас". Както и в предишния случай, елементарният резултат от теста е да се получат различни комбинации от шест букви. Общият брой на резултатите от всички изпитвания е равен на броя на пермутациите от 6, тъй като различните проби може да се различават една от другасамо по ред:
n=
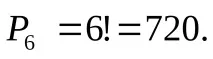
Думата "ананас" може да се получи по повече от един начин, тъй като пренареждането на три букви "а" и две букви "н" не променя тази дума. Три карти с буквата "а" могат да бъдат подредени по 6 начина:
m1=
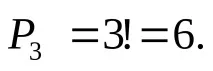
Две карти с буквата "n" могат да бъдат подредени по 2 начина:
m2=
Карта с буквата "с" може да бъде подредена по един начин. Тогава:m=m1m2m3=6 2 1=12. Следователно:
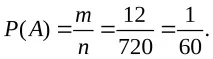
ПРИМЕР 2.3.В една урна има 15 топки, 9 от които са червени и 6 са сини. Каква е вероятността две произволно изтеглени топки: а) и двете да са червени; б) 1 червена, 1 синя?
РЕШЕНИЕ. а) Нека събитиетоА- изтеглени са две червени топки. Общият брой на резултатите от всички тестове е равен на броя начини, по които могат да бъдат избрани 2 топки от 15. Различните проби могат да се различават една от друга само по състав (редът няма значение), следователно:
n=
Броят на случаите в полза на събитиетоAе равен на броя комбинации от 9 червени топки по 2 всяка:
m=
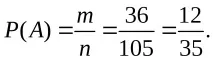
б) Нека събитиетоB- извадени са една червена и една синя топка. Общият брой на всички резултати от изпитанията, както в предишния случай, еn=105. За да изчислите броя на случаите, които благоприятстват събитиетоB, трябва да изберете 1 топка от 9 червени (един първоначален сет) и 1 топка от 6 сини (друг първоначален сет). Тогава:
m=m1m2=
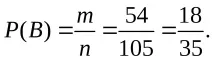
ПРИМЕР 2.4.Има 50 части в партида, 5 от тях са дефектни. Каква е вероятността две от шестте части, избрани на случаен принцип за тестване, да бъдат дефектни?
РЕШЕНИЕ. Нека е избрано събитиеА- 2дефектни части и 4 недефектни части. Общият брой на резултатите от всички тестове е равен на броя начини, по които могат да бъдат избрани 6 части от 50. Различните проби могат да се различават една от друга само по състав (редът няма значение), следователно:
n=
За да се изчисли броят на случаите, благоприятстващи събитиетоА, е необходимо да се изберат 2 части от 5 дефектни (един оригинален комплект) и 4 части от 45 недефектни (друг оригинален комплект). Тогава:
m=m1m2=
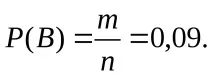
ПРИМЕР 2.5.Четирима души влязоха в асансьора на първия етаж на девететажна сграда, всеки от които може да излезе независимо един от друг на всеки етаж от първия до деветия. Каква е вероятността всички пътници да слязат: а) на шестия етаж; б) на същия етаж?
РЕШЕНИЕ. а) Нека събитиетоА- всички пътници ще напуснат шестия етаж. Всеки пътник може да слезе на осем етажа (от втория до деветия етаж), тоест оригиналният комплект се състои от 8 етажа. Пробата е равна на 4 етажа. Тогава общият брой на всички резултати от теста е равен на броя на поставянията с повторения, тъй като елементите на извадката могат да се повтарят (например и четиримата души могат да излязат на един и същи етаж). Ето защо:
n=
Броят на случаите в полза на събитиетоAе равен наm=1.
б) Нека събитиетоB- всички пътници слизат на един етаж. Сега събитие B ще бъде предпочитано отm=8 случая (всички пътници ще слязат или на втория етаж, или на третия, ... или на деветия етаж). Следователно:
ПРИМЕР 2.6.Има 100 продукта в партида, 4 от тях са дефектни. Партидата се разделя произволно на две равни части, които се изпращат на двама потребители. Каква е вероятността всички да са дефектничасти ще отидат за: а) един потребител; б) еднакво за двата потребителя?
РЕШЕНИЕ. а) Нека събитиетоA- всички дефектни продукти ще отидат при един потребител. Общият брой на резултатите от всички тестове е равен на броя начини за избор на 50 продукта от 100, тоест:
n=
СъбитиеAсе предпочита от случаите, при които от 50 артикула, изпратени до един потребител, ще има или 46 стандартни артикула от 96 и всичките 4 дефектни артикула, или 50 стандартни артикула от 96:
б) Нека събитиетоB- във всяка партида от 2 дефектни продукта. Сега събитие B ще бъде предпочитано от случаите, при които от 50 артикула, изпратени до един потребител, ще има 48 стандартни от 96 и 2 дефектни от 4, т.е.