Изопериметричен проблем и някои други максимални и минимални проблеми
Думата „изопериметричен“ идва от думите „isos“ (на гръцки „равен“) и „периметър“. Изопериметричната задача (в равнината) е да се намери фигурата, която има най-голяма площ сред всички фигури с еднакъв периметър. Решението на изопериметричната задача е и решение на друга задача, а именно: да се намери фигурата с най-малък периметър сред всички фигури с еднакъв размер.
Наистина, нека сред фигурите с периметър най-голямата площ - фигурата и тази площ е равна на Нека разгледаме произволна друга фигура със същата площ. Нека нейният периметър е. Помислете за фигура, подобна на нея с периметър от площта на фигурите и са свързани по същия начин като квадратите на периметрите, т.е. следователно площта на фигурата е равна Тъй като нейният периметър, по предположение, е равен на нейната площ е по-малка от тази на фигурата, тоест по-малка от A, което означава, че се оказва, че фигурата има по-малък периметър от всяка друга фигура със същия размер.
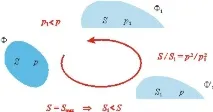
Като цяло, тъй като площите на подобни фигури са пропорционални на квадратите на периметрите, всички те имат една и съща стойност S / p 2, а за фигури с различни форми тази стойност може да се различава. За фигури, представящи решението на изопериметрична задача (независимо от размера), стойността на S / p 2 трябва да бъде най-голямата. (По-нататък ще наричаме това количество изопериметричен коефициент).
Имайте предвид, че проблемът с най-малката площ от фигури със същия периметър няма много смисъл: например, за даден периметър p, една от страните на правоъгълника ( a ) може да бъде направена по-малка и по-малка, докато другата му страна, равна на ( p / 2 - a ), е ограничена отгоре с p / 2, което означава, че площта на тази фигура няма да бъде повече от ap / 2. Дори ако, например, p = 1 000 000 km, е възможно да се направи площ S 2, ако поставим a = 2∙10 –8 mm; ако трябва да получите още 1000 пъти по-малкоплощ, също така е необходимо да се намали a с 1000 пъти и т.н. По този начин няма минимална площ за даден период: площта може да се различава от нула произволно малка.
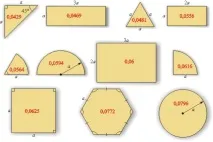
По аналогия с посочената изопериметрична задача върху равнина може да се разгледа и пространствена изопериметрична задача: кое триизмерно тяло от всички тела с еднаква повърхност има най-голям обем. Древногръцките математици вече са знаели отговора на изопериметричния проблем: в плоския случай желаната фигура е кръг (а в пространствения случай е топка). Тази идея се подсказва, първо, чрез пряко сравнение на площите на някои фигури с еднакъв периметър (или еднаква повърхност). Вижте зависимостта на изопериметричния коефициент от формата на равнинни фигури.
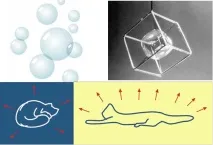
Второ, някои физически съображения също показват, че отговорът на изопериметричния проблем е кръг или сфера. Например, водните капки и сапунените мехурчета са сферични по причина: силите на повърхностното напрежение действат, за да намалят повърхностната площ. Характерно е също, че котките, когато е студено, спят, свивайки се колкото е възможно повече на топка: по този начин те намаляват повърхността на тялото, тъй като колкото по-малка е повърхността, толкова по-малко топлина изразходват във външното пространство.
Трето, древните гърци са смятали кръга за най-съвършената фигура (той е възможно най-симетричен, това е формата, която имат небесните тела и техните орбити). Това съображение увеличи тяхната увереност, че кръгът, в допълнение към другите си интересни свойства, също трябва да бъде решение на изопериметричния проблем.
Но геометрично древните гърци не можаха да докажат това, въпреки че стигнаха до редица конкретни, но важни резултати по тази тема, включително при решаването на различни проблеми закоя фигура от даден вид при дадени условия има най-голяма площ. Изследвания от този вид имаха не само теоретично, но и практическо значение: при разделянето на земята в древни времена понякога се извършваше измама, свързана с издаването на парчета от голям периметър и малка площ; периметърът е по-лесен за измерване от площта, така че някои лековерни клиенти прецениха размера на земята около периметъра.
Вероятно един от най-простите резултати по темата за изопериметричните фигури е теоремата, че от всички правоъгълници с еднакъв периметър квадратът има най-голямата площ. Наистина, нека периметърът на всички разглеждани правоъгълници е равен на 4 a и този правоъгълник има две големи страни, равни на ( a + x ) всяка, и две по-малки, съответно ( a - x ). Тогава площта на правоъгълника е ( a + x ) ( a - x ) = a 2 - x 2 , тоест не е по-малка от a 2 и достига максималната си стойност, когато правоъгълникът е квадрат със страна a .
В "Елементите" на Евклид има една единствена задача за максималната площ. В даден триъгълник ABC се изисква да се впише успоредник ADEF с най-голяма площ. Опитайте експериментално да намерите желания успоредник.
Отговорът на този проблем е следният: успоредникът има най-голяма площ, когато точка D разполовява страната BC. Евклид доказва този резултат с помощта на подобни триъгълници. На пръв поглед изглежда, че този проблем няма много общо с изопериметричните задачи: всъщност периметрите на разглежданите успоредници не са равни един на друг. Ако обаче "преместим" върха B успоредно на страната AC, тогава площите на успоредника ADFE и триъгълниците ABC, DEB и FEC няма да се променят (защото техните височини и основи няма да се променят). Задача приТова се свежда до следното: впишете правоъгълник с най-голямата площ в даден правоъгълен триъгълник.
По-нататък: ако този правоъгълен триъгълник е пропорционално компресиран или разтегнат по протежение на един от краката, така че краката да станат равни, тогава височините на тези правоъгълници и триъгълници ще се променят в същото съотношение и проблемът ще приеме следната форма: впишете правоъгълник с най-голямата площ в този правоъгълен равнобедрен триъгълник.
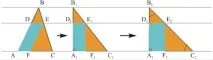
Този проблем е напълно изопериметричен: лесно е да се види, че всички разглеждани правоъгълници имат еднакъв периметър - когато едната страна се увеличава, другата намалява също толкова. Но вече знаем решението на изопериметричната задача за правоъгълници, това е квадрат и неговият връх дели хипотенузата на равнобедрен правоъгълен триъгълник наполовина. Това означава, че в първоначалната задача върхът на желания успоредник разделя съответната страна на триъгълника наполовина.
Зенодор (II в. пр. н. е.) е написал цял трактат "За изопериметричните фигури". Въпреки че трактатът на Зенодор не е оцелял, някои от резултатите му са достигнали до нас в изложението на математиците Пап (3 век сл. н. е.) и Теон (4 век сл. н. е.), включително следните теореми:
от два триъгълника с обща страна и равни периметри, принадлежи площта на този, който притежава най-големия от четирите ъгъла, съседни на тази страна (веднага следва, че от всички триъгълници с равен периметър с обща основа, площта е максимална за равнобедрен триъгълник);
с еднакъв брой страни и равни периметри, площта на правилния многоъгълник е по-голяма от неправилната;
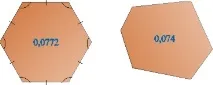
от два правилни многоъгълника с равни периметри, площта на този с повече страни е по-голяма.
Така че колкото по-близомногоъгълник към окръжност, толкова по-голям е неговият изопериметричен коефициент.
Невъзможно е да не споменем един много древен проблем, известен като проблема на Дидо. Според древен мит, възпроизведен в поемата на Вергилий "Енеида", бъдещата основателка на Картаген - Дидона (вероятно 9 век пр. н. е.) - избягала от преследването на брат си, тиранина на финикийския град Тир, на кораб с малък отряд хора, посветени на нея. Те акостираха на северноафриканския бряг, донесоха богати дарове на местния крал и поискаха парцел; кралят се съгласява да даде само „колкото земя заема една волска кожа“. Тогава Дидо направи дълъг тънък колан от кожата и огради с него значителна територия на морския бряг, където възникна град Картаген. Проблемът на Дидо традиционно се нарича проблемът каква форма трябва да има този участък, за да заеме най-голямата площ за дадена дължина на колана. Разгледайте този проблем за случая, когато брегът е прав. Нека коланът има дължина L и опасва определена фигура Ф1. Отразете го спрямо брега. Тогава коланът и неговото отражение заедно образуват границата (с дължина 2 L) на нова фигура F2, съставена от фигурата F1 и нейното отражение. Ако решението на изопериметричната задача е кръг, то площта Ф2 (за даден периметър 2 L ) е максимална, когато Ф2 е кръг. Но тъй като площта на Ф2 е точно 2 пъти по-голяма от тази на Ф1, площта на Ф1 също е максимална, ако Ф2 е кръг, а коланът, съответно, образува полукръг.