Изпаряване (сублимация)

При умерени температури и налягания, не твърде близки до критичните, обемът на кипящата течност е малък в сравнение с обема на сухата наситена пара, така че промяната в обемаV=Vn -Vw в уравнението на Клаузиус може да бъде заменена с обемаVP- суха наситена пара. Уравнението на Клаузиус-Клапейрон в този случай ще приеме формата

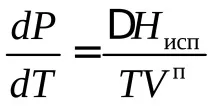
Ако при умерено налягане уравнението на идеалния газ на състояниетоPV=RTе приложимо за суха наситена пара, заместваме

и след това

,

.

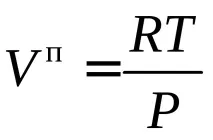
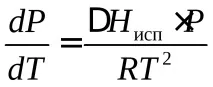
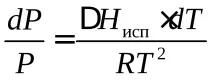
Въз основа на разсъжденията може да се получи уравнението на Клаузиус-Клапейрон за процеса на сублимация, което е приблизително. Предимството му е в лекотата, с която може да се интегрира

.

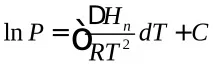
На диаграмата в координатите lnP– 1/Tтова уравнение се изразява с права линия с тангенс на ъгъла на наклон към оста 1/Tравен на –

.

Това обстоятелство може да се използва за намиране на приблизителната стойност на средната моларна топлина на изпаряване (сублимация) в определен температурен диапазон.

Интегрирането на приблизителното уравнение на Клаузиус при предположението, чеНне зависи отTв рамките наР1–Р2дава

Това уравнение е приемливо за използване в малък температурен диапазон.

Пример 1.Нормалната точка на кипене на йода е 185 0 С. Приблизително до каква температура трябва да се нагрее йодът в апарат под налягане, за да може да се дестилира?

Нека използваме уравнението на Клапейрон-Клаузиус

. (4)

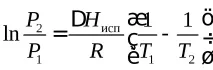
Уравнението дава моларната топлина на изпарение (Нexp), а в условието на задачатаспецифична топлина на изпарение, но

Нека преведемt0 C вTK.T= 185 0 C + 273 = 458K.

Заместваме наличните данни в уравнение (4) и решаваме заT2.

,

;

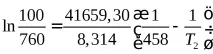
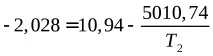
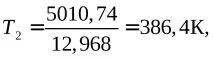
t0 С = 386.4 - 273 = 113.4 0 С.

Заключение. При налягане 100 mm Hg йодът ще кипи при температура 113,4 0 C.

Пример 2.При атмосферно налягане диетиламинът кипи при 58 0 C. При какво налягане ще кипи диетиламинът при 20 0 C, ако нормалната топлина на изпаряване е 27844,52 J/mol?

Нека използваме уравнението на Клапейрон-Клаузиус

. (4)

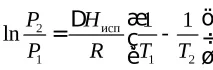
Нека преведемt0 C вTK.

Заместете данните в уравнение (4) и решете заP2.

,

,

Заключение. При налягане, равно на 208,5 mm Hg. диетиламинът ще кипи при 20 0 С.

Пример 3.Налягането на парите на кристалния ацетилен при 132K е 1,7 mmHg, а при 153K е 27,6 mmHg. Изчислете моларната топлина на топене на ацетилена, ако неговата специфична топлина на изпарение е 828,014 J/g.

Според условието ацетиленът преминава от твърдо състояние в парообразно състояние, т.е.Нf.p=Нpl+Низползване. Нека използваме уравнението (4) Клаузиус-Клапейрон:

.

.

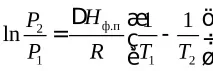
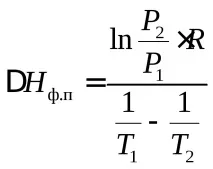
В задачата е дадена специфичната топлина на изпарение. Тя трябва да се преобразува в моларна топлина на изпаряване, тъй катоMr(С2Н2) = 26 g/mol

,

Нpl = 22281.44 - 21528.364 = 753.056

.

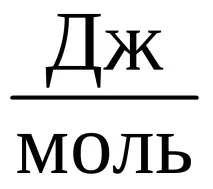
Заключение. Моларната топлина на топене на ацетилена е 753.056

.

---