Използване на MathCAD2000 и Microsoft Excel за прилагане на числени методи
Секции: Математика
При изучаване на дисциплината "Математика" в средни специализирани учебни заведения се предполага, че се разглежда темата: "Елементи на числените методи". Използването на MathCAD 2000 и Microsoft Excel за прилагане на числени методи позволява да се формира разбиране за математическото съдържание на конкретен метод и способността да се използват съвременни софтуерни инструменти. При използване на MathCAD 2000 и Microsoft Excel в хода на лабораторната работа студентите получават възможност да използват знанията, получени при изучаването на дисциплината "Информатика".
Възможностите на MathCAD 2000 ви позволяват да изграждате графики на зависимости, да разделяте графично корените на уравнения, да решавате уравнения и системи от уравнения, да трансформирате получените изрази, да проверявате правилността на полученото приблизително решение.
Възможностите на Microsoft Excel ви позволяват да не губите време за един и същ тип изчисления, бързо да коригирате грешки в изчисленията.
Използване на MathCAD 2000 и Microsoft Excel за приближено решаване на системи от линейни алгебрични уравнения чрез итерация.
На първия етап от приблизителното решение на SLAE по метода на простата итерация е необходимо системата да се приведе в нормална форма. За да направите това, трябва да изразите x от първото уравнение, y от второто уравнение и т.н. Това може да се направи с помощта на Math CAD 2000. В този случай може да се използва един от методите за решаване на уравнения: въвежда се уравнение, удебелен ( + ) се поставя равен и командатаsolveсе дава от панела „Символика“, след като посочите променливата, по отношение на която трябва да се разреши уравнението, ще получим резултата.
На втория етап от решението е необходимо да се провери за получената система, приведена до нормалната форма, условието за сходимост на итеративния процес, т.е.матрични норми с единица. Например, проверете условието най-голямата от сумите на модулите на елементите на колоната да е по-малка от 1. Това може да стане и с Math CAD 2000. Това използва функциятаnorm1(А)от стандартния набор от функции.
Итеративният процес е по-удобен за извършване в Microsoft Excel. Номерът на стъпката на итерация се въвежда в колона A, стойностите на xk, yk, zk се въвеждат в колони B, C, D; стойностите xk+1, yk+1, zk+1 се въвеждат в колони E, F, G; в колона H можете да изчислите стойността на грешката на изчислението на дадена стъпка на итерация, за да извършите изчисления с дадена степен на точност.
Когато попълвате клетки B3, C3, D3, по-добре е да се обърнете към клетки E2, F2, G2, вместо да въвеждате данни ръчно, това ще ви позволи да използвате по-добре времето, да използвате по-добре автоматичното довършване и да улесните коригирането на грешки.
Можете да проверите правилността на получените резултати чрез решаване на системата с помощта на MathCAD 2000. Това може да стане с помощта на командитеgivenиfind.
За да решите тази система по метода на Seidel, ще бъде достатъчно просто да промените формулите за изчисляване , yk, zk.
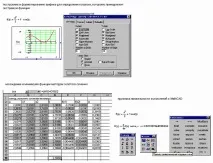
Пример за използване на MathCAD 2000 и Microsoft Excel за приблизително решаване на система от линейни алгебрични уравнения чрез прости итерации и метода на Seidel може да се види на фиг.1.

Използване на MathCAD 2000 и Microsoft Excel за кубична сплайн интерполация
Сега използването на кубични сплайн функции, които са специално конструирани полиноми от трета степен, стана широко разпространено за интерполация.
При прилагането на този метод за функция, зададена от четири точки, е необходимо да се състави и реши система от девет уравнения с девет неизвестни. Тази система трябва да бъде изградена ръчно. Решете дали получената система е по-добра в MathCAD2000, това ще спести време и ще ви позволи бързо да коригирате възможните грешки. Това може да стане с помощта на командитеgivenиfind,или по матричен начин.
Можете да проверите коректността на сплайн интерполацията, като начертаете тази функция и получения сплайн в MathCAD 2000. За това са посочени X и Y матриците на първоначалните данни, три сегмента, върху които е изградена сплайн функцията. След това се задават и трите функции, които дефинират сплайн функцията (аргументът за всяка трябва да е различен, съответстващ на сегмента, върху който е построена тази функция). Последната стъпка е да начертаете графиката. Запетая се използва за указване на множество аргументи и функции. Ако щракнете 2 пъти върху полето на графиката, ще се появи прозорец за форматиране на графики, в разделаX-Y Axecможете да зададете линията на мрежата, а в разделаTracesможете да зададете типа на линията на графиката и да начертаете графика на първоначалните данни с точки, а графиката на получената сплайн функция с плътна линия.
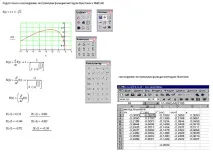
Пример за използване на Math CAD 2000 за кубична сплайн интерполация може да се види на фигура 2.

Шаблон, изготвен в MathCAD 2000, ще помогне на учителя бързо да изчисли вариантите за задачи (фиг. 3). Получените отговори ще помогнат бързо да се намери грешката, допусната от ученика, и да му помогнат да я коригира.

Използване на MathCAD 2000 и Microsoft Excel за намиране на екстремума на функция чрез метода на златното сечение
Когато решавате проблема за намиране на екстремума на функция по метода на златното сечение, първо трябва да определите сегмента, към който принадлежи минимумът или максимумът. Това може да стане чрез конструиране на графика на тази функция в MathCAD 2000. След като форматирате графиката, можете да посочите сравнително малък сегмент, към който принадлежи екстремумът на функцията.
По-добре е екстремалната стойност да се прецизира с определена степен на точноств Microsoft Excel. В колони A и D е удобно да въведете стойността на краищата на сегмента на дадена стъпка, а в колони B и C - формули за намиране на точки, които извършват златното сечение на този сегмент. Колоните E и F изчисляват стойностите на функцията в тези точки, а колоната G изчислява дължината на разглеждания сегмент, т.е. точността на изчислението на тази стъпка. За по-голяма яснота, изборът на следващия разглеждан сегмент, можете да маркирате клетките с цвят. Следващите редове се попълват чрез автоматично довършване.
Коректността на решението може да се провери в MathCAD 2000. За целта е необходимо да се използват правилата за намиране на екстремума на функция чрез математически анализ. За да намерите производната на функция и да решите полученото уравнение, панелите за смятане и символи ще помогнат.
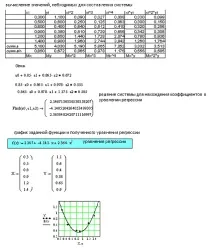
Пример за използване на MathCAD 2000 и Microsoft Excel за намиране на екстремума на функция чрез метода на златното сечение може да се види на фиг.4.
Използване на MathCAD 2000 и Microsoft Excel за намиране на екстремума на функция по метода на Нютон
При намиране на екстремума на функция по метода на Нютон, MathCAD 2000 ще помогне не само да се определи сегментът, към който принадлежи екстремумът, но и да се изчислят първата, втората, третата производна, необходими за избор на първоначалното приближение и техните стойности в краищата на разглеждания сегмент.
Можете да намерите екстремум с дадена степен на точност в Microsoft Excel. Колона A съдържа първоначалната стойност на екстремума, колони B и C изчисляват стойностите на първата и втората производни в тази точка. В колона D се изчислява уточнената стойност на екстремума, като се използва формулата на Нютон, а в колона E се изчислява точността на изчислението на дадена стъпка.
Пример за използване на Math CAD 2000 и Microsoft Excel за намиране на екстремума на функция по метода на Нютон може да се види нафиг.5
Използване на MathCAD 2000 и Microsoft Excel за напасване на функции чрез метода на най-малките квадрати
Когато извършвате линейно приближение на функции по метода на най-малките квадрати, за да съставите регресионно уравнение, първо трябва да изчислите числата Мх, Мху, Му, Мх 2 , удобно е да направите това в Microsoft Excel с помощта на автоматично сумиране.
Въз основа на получените стойности на Mx, Mx, My, Mx 2 се съставя система, след решаването на която ще бъде възможно да се запише регресионното уравнение. Можете да решите системата с помощта на MathCAD 2000.
Коректността на изчисленията може да се провери в MathCAD 2000. Функциите interсept(X,Y) и slope(X,Y) изчисляват стойностите a0 и a1 от дадените вектори на експериментални данни X, Y, за да напишат уравнението на линейната регресия във формата j (x)=a0+a1x.
След това, като използвате MathCAD 2000, можете да се уверите, че полученото регресионно уравнение приближава таблично зададената функция, като начертаете тази функция и полученото регресионно уравнение в една и съща координатна система. Възможности
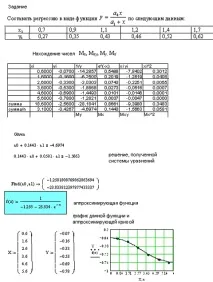
Пример за използване на MathCAD 2000 и Microsoft Excel за съставяне на уравнение на линейна регресия може да се види на фиг.6.

По подобен начин MathCAD 2000 и Microsoft Excel се използват за извършване на апроксимация на функции чрез полиноми от втора степен и съставяне на регресионни уравнения, които се преобразуват в линейни. Примери за това са показани на Фигура 7 и Фигура 8.
Използване на MathCAD 2000 за числено решаване на диференциални уравнения по метода на Runge-Kutta
Реализирането на численото решение на диференциалното уравнение по метода на Рунге–Кута, дори и в Microsoft Excel, е много времеемък процес. MathCAD 2000 улеснява тази задача.
Можете да решите диференциално уравнение с помощта на метода Runge–Kutta в MathCAD 2000по два начина: използване на вградена функция и директно използване на формули.
При директното прилагане на метода Runge-Kutta се задават формули за изчисляване на необходимите коефициенти и след това се създава цикъл за изчисляване, като се използват желаните от тях стойности на y.
Вградената функцияrkfixedви позволява да приложите метода Runge–Kutta, без да извършвате изчисления. С тази функция можете да поканите учениците да проверят изчисленията, които са извършили с помощта на формули, а учителят бързо да изчисли различните опции.
Пример за използване на MathCAD 2000 за прилагане на метода Runge-Kutta за числено решаване на диференциално уравнение може да се види на фигура 9.

Използването на MathCAD 2000 и Microsoft Excel за прилагане на числени методи и за решаване на други математически проблеми ще помогне на учениците не само да разберат по-добре методите за решаване на проблеми, без да губят време за рутинни изчисления, но също така ще създаде възможности за използване на тези програми в по-нататъшно образование и в професионални дейности.