Как да намерите позицията на камерата от три точки навътрепространство

Тези. имаме снимка, в този случай на стол. Струва ми се възможно, знаейки позицията на точките в пространството, знаейки координатите на същите точки на снимката (както и зрителния ъгъл на камерата), да се намери позицията на камерата. Но не разбирам как да подходя към този проблем. В главата ми се въртят фрагменти от мисли като "разрез на пирамидата", "централна проекция" и други "стереометрии".
Подскажете в каква посока да копаете? Скриптът ще бъде написан на третия питон, може би има някои полезни пакети?
Полиномът има само четни степени на z, коефициентът на z^8 е (a^2+b^2+c^2-2*a*b*c-1)^2. Чудя се какво е.
Mrrl: Не може да се каже, че всичко върви гладко, не е много стабилно. Може би грешката на изчисленията се натрупва, дуализмът на решенията на полином с четна степен може да повлияе. от пет точки обикновено 3 се определят приблизително нормално, 2 са плаващи - по-близката от двете точки може да се окаже по-отдалечена или като цяло точката излита от сцената.
Решението се извършва чрез замяна на полиномните променливи a1*z^8 + a2*z^6 + a3*z^4 + a4*z^2 + a5 = 0 с z1 = z^8, z2 = z^6, z3 = z^4, z4 = z^2 и след това изчисляване на обратната матрица на линейната система, съставена от тези 5 точки. Условията z3
Mrrl: На разстоянието Z беше обърнато внимание по начина, който споменахте - в противен случай вероятно нямаше да е възможно да се получат тези все още скромни, но надяваме се обещаващи резултати.
Кратността обаче не ме успокоява - тя се намира в уравненията на косинусовата теорема, геометрично можете да имате такава картина веднагапредставете си:
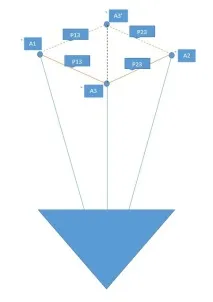
Mrrl: Струва ми се, че корените най-вероятно ще са близки, което следва и от геометричната илюстрация на проблема - точката n, разположена на dZ, по-близо или по-далече ли е от съседите си в популацията?
Не искам да вземам голям брой точки - в крайна сметка изчислителната сложност на алгоритъма е забележима, изчисляването на всички коефициенти на едно уравнение е около хиляда операции за добавяне и умножение, система от 4 часа за една точка, заедно с решението на обратната матрица - вече повече от 5 хиляди операции и трябва да работи в реално време на iPad / iPhone. Да, и референтните точки все още трябва да бъдат взети някъде, особено в първите повторения.
От друга страна, моделът не използва най-важното правило - центърът на камерата, точката в пространството и проекцията на точката да са на една права линия. Проекцията на точка може да бъде изразена в условни реални координати чрез пикселни координати в съответствие с матриците на въртене на камерата: y)*sin(Rz)+Uy*cos(Rx)*cos(Rz), -Ux*sin(Ry)-cos(Ry)*sin(Rx) ) където Rx,Ry,Rz са желаните стойности на ъглите на въртене на камерата (от позицията по Z ос), С е желаният център на камерата, U се изчислява от пикселните координати на точката като (tg(uv.x-W/2)/W* fov_x,tg(uv.y-H/2)/H*fov_y))
Опитах се да съставя линейна система чрез уравнението на права линия, като взех предвид данни за три точки - център на камерата, точка в пространството и проективна точка, но досега са получени само хомогенни системи, някъде трябва да вземете свободния термин.