Как учител по математика намира стойностите на тригонометричните функции
О, колко мъки дава на учениците изучаването на тригонометрията. Възникват определени трудности, дори акоучител по математика седи наблизо и дъвче всяко малко нещо. Това е разбираемо, само основните формули са повече от двадесет. И ако броим техните производни ... Наскоро начинаещ учител по математика изпрати писмо, в което поиска да говори за метода на практическа работа с формули за намаляване. Неговият ученик се обърква в изчисленията и не може да си спомни механизмите, чрез които тези формули позволяват да се намери напр. С голямо удоволствие изпълнявам молбата му.
Така че ще приемем, че учителят по математика е определил с ученика какво е синус и косинус, обяснил е радианите, свойствата на четните и нечетните тригонометрични функции, повторил е или е научил отново техниката на трансформации, използвайки формули за редукция. Какъв материал трябва да се демонтира след тези задължителни стъпки? Разбира се, трябва да научите как да изчислявате синуси и косинуси за ъгли, разположени извън първата четвърт. Сигурен съм, че опитен учител по математика няма да открие нищо ново в алгоритъма от гледна точка на математиката, но може да направи някои корекции по отношение на методологията.
Дълго време третирах описаната по-долу техника като единствената в тази тема, докато не срещнах различни грешки в подходите на други преподаватели по математика и учители (чрез училищните тетрадки на моите ученици). Оказва се, че някои учители например превръщат ъглите в градуси и пресмятат през тях.
Предпочитам да започна веднага с вариант, в който всички точки от общия алгоритъм ще трябва да бъдат изпълнени. Защо? Основната работа на учителя по математика трябва да бъде насочена към запаметяване на техниката, тъй като семантичната работа остава вобхванати теми, когато се изучаваха дефинициите на тригонометрични функции, формули за редукция и операции с ъгли.
Поради тази причина учителят по математика трябва да започне с пример, в който има отрицателен ъгъл под знака синус.
1) Ученикът премахва знака минус върху свойството четно/нечетно. Това е задължителна и приоритетна операция. Ако извършим допълнителни трансформации заедно със знака, тогава учителят по математика ще загуби възможността да даде ясни и удобни описания на операциите с радиани в по-нататъшните етапи на своя алгоритъм. Премахването (премахването) на знак от учениците обикновено се извършва безпроблемно, ако се запомнят съответните свойства. Ако преподавател по математика посочи, че косинусът е единствената изучавана четна функция, тогава няма да има никакви проблеми.
2) Премахване на "пълни обороти". Учителят показва как можете да замените положителен ъгъл с такъв, който е между 0 и . За да направите това, цялата част се отделя от фракцията. В този случай буквата се намира под формата на множител до правилната фракция, тоест се оказва. Тъй като при изваждане на пълен завой от този ъгъл, т.е. ъгълът, ние изваждаме 2 от коефициента 5, за учителя по математика няма да е трудно да предаде на детето логиката на многократното изваждане на „пълен завой“, тоест изваждане от 5най-близкото четно число към него. За да демонстрирам алгоритъма, нарочно избирам ъгъл, в който остава цялата част, равна на единица. Защо? Ако учителят по математика започне от нула цели числа, тогава важен етап от алгоритъма ще се изплъзне от зрителното поле на ученика: преобразуването на получения коефициент в неправилна дроб за сравнение с основните ъгли. Един слаб ученик едва ли ще познае това сам. В резултат на това все още трябва да разглобяватеопция с едно и загуба на допълнително време. По-добре е да го използвате за самостоятелна работа на ученика.
3) Преобразуване на дроб в неправилна:. Важно е да премахнете цялата част, така че да не пречи на по-нататъшните сравнения.
4) Определяне на четвъртината, в която лежи ъгълът. За да направите това, трябва да го сравните с основните ъгли, като ги приведете към общ знаменател. Как учителят по математика улеснява работата на ученика? Има 4 ъгъла: . Ако се изучава ъгъл със знаменател 3, тогава, като се има предвид необходимостта от сравнението му, и двата знаменателя ще трябва да бъдат променени на 6. Това не е много удобно. Какво решение предлага учителят по математика за сравнение? Необходимо е да се изключат дробните основни ъгли от процеса. Защо? За да определи тримесечието, учителят ще има достатъчно и. По-удобно е да ги настроите към всеки знаменател на изучавания ъгъл от задачата. В нашия пример получаваме и . Ясно е, че е по-близо до, отколкото до. Следователно въпросът за една четвърт отпада. Горд съм да кажа, че в цялата история на ученика не е пропуснал отговор на въпроса за тримесечието след такава подготовка. Ако учителят по математика откаже да преобразува предишния коефициент в неправилна дроб, тогава ще бъде по-трудно да се определи една четвърт.
Учителят по математика се задължава да илюстрира решението.
Горещо препоръчвам да маркирате получения ъгъл върху тригонометричния кръг, след като бъде определена неговата четвърт.
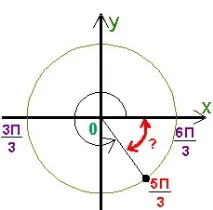
7) Останалото е въпрос на технология. Ученикът премахва чрез формулата за намаляване и се позовава на таблицата със синусови стойности за остър ъгъл.
Извод : За съжаление дидактиката на всички учебници без изключение относно изчислителната част с радиани е много куца. Всичко, което учителят може да намери, са едно или две числа, които комбинират задачи за градуси и радиани. Но търсенето, например, е много по-лесно от еквивалентното броене в радиани. Не съветвам учителите по математика да превеждат ъглите в градуси, тъй като всички основни операции в тригонометрията се извършват в радиани и в тази връзка описаната по-горе практика на работата на ученика ще бъде добра подготовка за бъдещи задачи за него.
За съжаление учителят по математика няма право да избира учебник. Училището го прави вместо него. Жалко, тъй като последователността на разбор на темите по тригонометрия в някои от тях, меко казано, не е идеална. Преди изучаването на формулите за редукция се разглеждат тригонометричните уравнения. И не само уравнения. Децата все още не са разбрали наистина как се изчисляват синус и косинус и вече им се налагат формули за двоен ъгъл.
Александър Николаевич, учител по математика и тригонометрия. Москва.
Аз също съм против превръщането на радианите в градуси - трябва да се научите да броите и двата начина. Но някои от моите ученици конвертират от радиани в градуси и обратно много по-бързо и извършват различни математически операции по-бързо с градуси, отколкото с радиани. Това се отнася само за формулите за редукция, тъй като за някои хора е трудно веднага да разберат през кой главен ъгъл е по-лесно да се изрази дробният радиан. На менизглежда, че ако студентът успее по-бързо със степените, тогава учителят по математика няма какво да му наложи в противен случай. Освен това изпитът няма гумено време.