КАРТИРАНЕ ПО ПОАНКАРЕ
В математическото изследване на динамични системи картографирането е временна извадка от данни, за която се въвежда обозначението
В просто детерминистично картографиране стойността може да бъде намерена от стойността на . Това често се пише като
В такъв запис можете да намерите уравнението на разликата. Понятието картографиране може да се обобщи за по-голям брой променливи. И така, може да бъде вектор с M компоненти; , и тогава уравнение (2.2) ще бъде система от M уравнения.
Да предположим например, че анализираме движението на частица, изобразена на фазовата равнина.Ние вече знаем, че ако движението е хаотично, тогава траекторията се стреми да запълни определена област от фазовото пространство. Ако обаче, вместо непрекъснато наблюдение на движението, ние фиксираме динамичните характеристики само в отделни моменти, тогава движението ще бъде представено чрез последователност от точки във фазовата равнина (фиг. 2.8). Ако , тогава тази последователност от точки на фазовото пространство е двумерно картографиране
Ако моментите на вземане на проби се подчиняват на определено правило, обсъдено по-долу, това картографиране се нарича картографиране на Поанкаре.
Картографиране на Поанкаре за системи с принудени трептения. Когато има принудително движение с период T, естествено е да се избере проба с, за да се получи картографирането на Поанкаре. Това дава възможност да се разграничат периодичните движения от непериодичните.
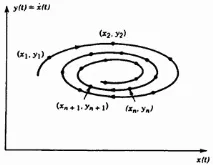
Ориз. 2.8. Схематична илюстрация на еволюцията във времето на точките на Поанкаре от извадка от цифрови измервания.
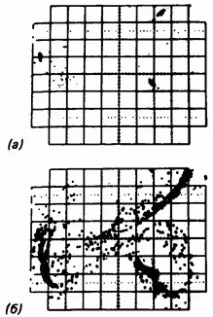
Ориз. 2.9. а — Картиране на Поанкаре във фазовата равнина, съответстващо на субхармонично движение с период 3 на надлъжно извита пръчка, възбудена от периодичен сигнал; b - хаотично движение близо до третатасубхармоници.
Например, ако образецът на хармоничното движение, показан на фиг. 2.4, а, синхронизирайте с неговия период, тогава "дисплеят" ще бъде представен от две точки на фазовата равнина. Ако обаче отговорът съдържаше субхармоник с период 3, тогава картата на Поанкаре ще се състои от трите точки, показани на фиг. 2.9, а. (За да използваме жаргона на математическата теория на динамиката, се казва, че картата (2.3) с функциите f и g има три фиксирани точки.)
Друга нехаотична карта на Поанкаре е показана на фиг. 2.10, където движението е трептене на две несъизмерими честоти:
където е ирационално число. Ако направите проба с период, съответстващ на една от честотите, тогава траекторията ще стане непрекъсната затворена фигура или орбита на фазовата равнина. Такова движение понякога се нарича почти периодично, или квазипериодично, или "движение по тор"; не е хаотично.
И накрая, ако картографирането на Поанкаре не се състои от краен набор от точки (виж фиг. 2.9, а) или затворена орбита (виж фиг. 2.10), тогава съответното движение може да бъде хаотично (фиг. 2.11). На този етап трябва да се прави разлика между системи със и без демпфиране. В системи без затихване или със слабо затихване, картите на Поанкаре на хаотичните движения често изглеждат като неподредено натрупване на точки във фазовата равнина (фиг. 2.11, а).
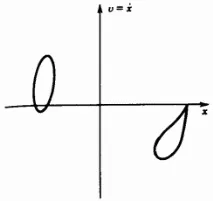
Ориз. 2.10. Картографиране на Поанкаре във фазовата равнина, съответстващо на квадрипериодичното движение на прът, възбуден от периодичен сигнал с две степени на свобода, който осцилира в двойка потенциални ямки, създадени от магнитни сили.
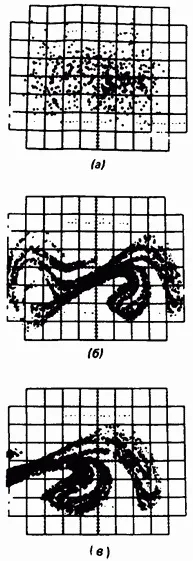
Такива движения понякога се наричат стохастични (вижте например [110]). В системи с избледняване на картата на Поанкарепонякога те са безкрайни строго подредени набори от точки, концентрирани върху сходството на успоредни линии, както е показано на фиг. 2.11, b, c. При числена симулация е възможно да се увеличи частта от картата на Поанкаре (фиг. 2.12) и да се намери по-фина структура. Ако тази точкова структура се запази след няколко увеличения, тогава се казва, че движението се държи като странен атрактор. Множества с подобно вграждане на една структура в друга често се наричат множества на Кантор (виж глава 6).
Появата в картографирането на Поанкаре, което изобразява времевата еволюция на трептенията, на структури, които са подобни на набора на Кантор, е силен индикатор за хаотични движения.
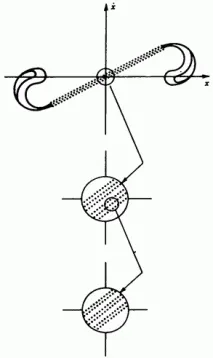
Ориз. 2.12. Картографиране на Поанкаре за хаотични трептения на възбуден нелинеен осцилатор, запазвайки самоподобната структура на все по-малки мащаби.
Класовете структури, които се срещат в преобразуванията на Поанкаре, са изброени в таблица 1. 2.2.
Таблица 2.2. Класификация на преобразуванията на Поанкаре

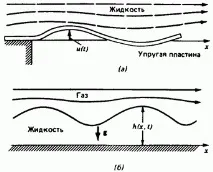
Ориз. 2.13. Примери за самовъзбуждащи се трептения: а - поток на течност върху еластична плоча; b - газов поток над повърхността на течността.
Преобразуване на Поанкаре за автономни системи. Стационарните трептения могат да бъдат възбудени без периодични или произволни влияния и ако движението се генерира от динамична нестабилност, като трептения на еластична структура, предизвикани от поток от вятър (фиг. 2.13) или конвективно движение на течност или газ, създадено от температурен градиент (например, конвекция на Бенард - вижте фиг. 1.23). В електрическите системи или системите за управление с обратна връзка могат да възникнат трептения от самовъзбуждане поради елементи с отрицателна стойностсъпротива или отрицателна обратна връзка. Тогава възниква въпросът в кои времеви точки трябва да се правят измервания, за да се получи картата на Поанкаре. Ще обсъдим този въпрос на малко по-абстрактен език.
Да разгледаме хаотична система от най-нисък порядък, описана от три диференциални уравнения от първи ред (например уравненията на Лоренц от глава 1). В случай на електромеханична система, променливите x(t) могат да имат значението на преместване, скорост и управляваща сила, ако това е система за управление със затворен контур. Движението може да бъде представено като траектория в тримерното фазово пространство (фиг. 2.14). Картата на Поанкаре може да се определи чрез конструиране на двуизмерна ориентирана повърхност в това пространство и следене на точките, в които траекторията минава през тази повърхност. Нека изберем например равнина с нормален вектор
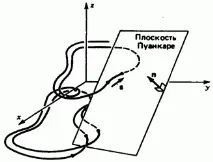
Ориз. 2.14. Схематично представяне на траекториите на система от уравнения от трети ред и типична равнина на Поанкаре.
Като специален случай може да се избере равнината x = 0. Тогава картата на Поанкаре се състои от тези точки на равнината, през които траекторията минава в една и съща посока, т.е. ако е единичен вектор, допирателен към траекторията, тогава скаларното произведение трябва винаги да има същия знак.
Дефиницията на преобразуването на Поанкаре се разширява и до случая, когато върху системата действа периодична външна сила. Като пример, разгледайте принудените нелинейни трептения, описани от уравненията на движението:
Тази система може да бъде доведена до автономна форма чрез въвеждане на определението
Сега можем естествено да изберем онези моменти на вземане на проби, при които z = 0. За тази система фазовото пространство имацилиндрична форма с ограничени z стойности: . Конструкцията на отображението на Поанкаре е показана на фиг. 2.15.
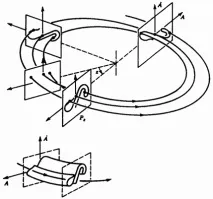
Ориз. 2.15. Схематично представяне на странен атрактор за принудителни трептения на нелинеен осцилатор е "продуктът" на равнината на Поанкаре и фазата на вълнуващия сигнал.
Намаляване на динамичните модели до едномерни преобразувания. В гл. 1, видяхме, че простите едномерни преобразувания или диференциалните уравнения на формата могат да съдържат бифуркации и хаос при удвояване на периода, ако функцията има поне един максимум (или минимум), както е показано на фиг. 1.19. Явленията на удвояване на периода са наблюдавани в много различни сложни физически системи (течности, лазери, електронни преходи); и често динамиката на тези системи е добре описана чрез едномерни картографии. Тази възможност е особено характерна за системи със значително затихване. За да се тества тази възможност, трябва да се вземе проба от някаква динамична променлива, като се използва разделът на Поанкаре, обсъден по-горе, да речем. Тогава може да се начертае зависимостта на всяка от следващата стойност на . За да бъде обявена една система за хаотична, трябва да бъдат изпълнени два критерия. Първо, точките на графиката със стойности, нанесени по осите, трябва да бъдат групирани, създавайки някакъв вид функционална зависимост; второ, тази функция трябва да бъде немонотонна, тоест трябва да има максимум или минимум. Ако тези изисквания са изпълнени, тогава трябва да се избере полиномна апроксимация на получените точки и да се използва намерената карта за по-нататъшни числени експерименти или анализ, подобен на анализа на квадратна карта (глави 1 и 5).
Примери за използване на тази техника са изследването на течащ кран [171] и експериментът с варикап диод в електрическа верига [162] (вижте същообсъждане на тези проблеми в гл. 3). В гл. 4 ще продължим обсъждането на тази техника.