KNOW INTUIT, Лекция, Алгоритми върху графики
Първо търсене в дълбочина
При търсене в дълбочина се посещава първият връх, след което е необходимо да се върви по краищата на графа, докато се стигне до задънена улица. Върхът на графиката езадънена улица, ако всички върхове, съседни на него, вече са били посетени. След като се стигне до задънена улица, човек трябва да се върне обратно по изминатия път, докато се намери връх, който има непосетен връх, след което е необходимо да се придвижи в тази нова посока. Процесът завършва при връщане към първоначалния връх, като всички съседни на него върхове трябва вече да са били посетени.
По този начин основната идея на търсенето в дълбочина е, че когато възможните пътища по ръбовете, излизащи от върховете, се разклоняват, първо трябва да се изследва напълно един клон и едва след това да се премине към други клонове (ако останат неизследвани).
Алгоритъм за първо търсене в дълбочина
Стъпка 1. На всички върхове на графиката се присвоява непосетената стойност. Първият връх е избран и маркиран като посетен.
Стъпка 2. За последния връх, маркиран като посетен, се избира съседният връх, който е първият маркиран като непосетен, и му се присвоява посетената стойност. Ако няма такива върхове, тогава се взема предишният маркиран връх.
Стъпка 3. Повторете стъпка 2, докато всички върхове бъдат маркирани като посетени (фиг. 44.5).
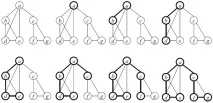
Времевата сложност зависи от представянето на графиката. Ако се приложи матрицата на съседство, тогава времевата сложност е O(n 2 ) , а ако нематричното представяне е O(n+m) : всички върхове и всички ръбове се вземат предвид.
Първо търсене в широчината
При търсене в ширина, след посещение на първия връх, се посещават всички съседни върхове. След това се посещават всички върхове, които са на разстояние дверъбове от първоначалния. При всяка нова стъпка се посещават върхове, разстоянието от които до началната стъпка е с един повече от предишната. За да се предотврати повторното посещение на върховете, трябва да се поддържа списък с посетени върхове. За съхраняване на временни данни, необходими за работата на алгоритъма, се използва опашка - подредена последователност от елементи, в която нови елементи се добавят към края, а старите се премахват от началото.
По този начин основната идея на търсенето в ширина е, че първо се изследват всички върхове, съседни на началния връх (върхът, от който започва преминаването). Тези върхове са на разстояние 1 от началния. След това се изследват всички върхове на разстояние 2 от първоначалния, след това всички на разстояние 3 и т.н. Обърнете внимание, че в този случай за всеки връх веднага се намира дължината на най-краткия маршрут от началния връх.
Алгоритъм за търсене първо в ширина
Стъпка 1. На всички върхове на графиката се присвоява непосетената стойност. Първият връх е избран и маркиран като посетен (и добавен към опашката).
Стъпка 2. Посещава се първият връх от опашката (ако не е маркиран като посетен). Всички негови съседни върхове се добавят към опашката. След това се премахва от опашката.
Стъпка 3. Стъпка 2 се повтаря, докато опашката се изпразни (фиг. 44.6).
Сложността на търсенето в ширина за представяне на не-матрична графа е O(n+m), тъй като се вземат предвид всички n върха и m ребра. Използването на матрица на съседство води до оценка O(n 2 ).
Ключови термини
Тегло (дължина) на ръбе число или няколко числа, които се интерпретират във връзка с ръба като дължина, капацитет.
Тегло на връхе число (реално, цяло число или рационално), присвоено на даден връх.
Претеглена графае графа, всяко ребро на която е свързано със своето тегло.
Графикае колекция от два крайни набора: набор от точки и набор от линии, които свързват по двойки някои от тези точки.
Върховете (възлите) на графикатаса набор от точки, които изграждат графиката.
Затворен маршруте маршрут в граф, чийто начален и краен върхове са еднакви.
Множество ръбовеса ръбове, свързващи една и съща двойка върхове.
Маршрут в графе крайна редуваща се последователност от съседни върхове и ръбове, свързващи тези върхове.
Матрица на инцидентносте двуизмерен масив, който показва връзките между инцидентните елементи на графиката (ръб и връх).
Матрица на съседствое двуизмерен масив, чиито стойности на елементи се характеризират със съседството на върховете на графиката
Мултиграфе граф, в който всеки два върха са свързани с повече от едно ребро.
Неориентиран граф (недиграф)е график, в който всички ребра са неориентирани, т.е. на чиито ребра не е дадена посока.
Насочен граф (диграф)е график, в който всички ребра са ориентирани, т.е. на чиито ребра е присвоена посока.
Отворен маршруте маршрут в граф, чийто начален и краен върхове са различни.
Примкае ребро, което свързва връх със себе си.
Първо търсене в дълбочинае обхождане на графика по възможни пътища, когато първо трябва да проучите напълно един клон и едва след това да преминете към други клонове (ако останат непроверени).
Първо търсене в ширинае обхождане на граф по възможни пътища, когато след посещение на върха, всичкивърхове, съседни на него.
Прост графике график, който няма нито цикли, нито множество ребра.
Пътяте отворена верига с различни върхове.
Ръбовете (дъгите) на графикатаса набор от линии, свързващи върховете на графиката.
Свързан графе граф, който за всяка двойка върхове има път, който ги свързва.
Съседните върховеса върхове, свързани с общ ръб.
Смесен графе график, съдържащ както насочени, така и ненасочени ребра.
Списък от ръбовее набор, образуван от двойки съседни върхове
Задънена улицае връх на графика, за който всички върхове, съседни на него, вече са били посетени
Веригатае маршрут в графика, където всички ребра са различни.
Цикъле затворена верига, в която всички нейни върхове са различни, с изключение на крайните.