KNOW INTUIT, Лекция, Дървообразни алгоритми за търсене
Оптимални дървета
В едно двоично дърво търсенето на някои елементи може да се случи по-често от други, т.е. има вероятности pk за търсене на k -тия елемент и тези вероятности не са еднакви за различните елементи. Може да се предположи, че търсенето в дървото ще бъде средно по-бързо, ако онези елементи, които се търсят по-често, са по-близо до корена на дървото.
Нека са дадени 2n+1 вероятности p1,p2. pn, q0,q1. qn, където pi е вероятността аргументът за търсене да е Ki елемент; qi е вероятността аргументът за търсене да се намира между върховете Ki и Ki+1; q0 е вероятността аргументът за търсене да е по-малък от стойността на елемента K1; qn е вероятността аргументът за търсене да е по-голям от Kn. Тогавацената на дървото за търсенеC ще бъде определена както следва:
където е нивото на възел j и е нивото на листа K.
Едно дърво за търсене се наричаоптимално, ако цената му е минимална. Тоест,оптималното двоично дърво за търсенее двоично дърво за търсене, изградено да осигури максимална производителност за дадено вероятностно разпределение на търсене на необходимите данни.
Съществува подход за конструиране на оптимални дървета за търсене, в които елементите се вмъкват в низходящ ред на честота, което дава средно добри дървета за търсене. Този подход обаче може да доведе до изродено дърво за търсене, което е далеч от оптималното. Друг подход е да се избере коренът k по такъв начин, че максималната сума от вероятности за върховете на лявото поддърво или дясното поддърво да е възможно най-малка. Този подход също може да бъде лош, ако изберете елемент с малка стойност на pk като корен.
Има алгоритми, които правят възможно конструиранетооптимално дърво за търсене. Те включват например алгоритъма на Garcia-Voch. Такива алгоритми обаче имат времева сложност от порядъка на O(n 2 ) . По този начин създаването на оптимални дървета за търсене изисква големи разходи, които не винаги оправдават печалбата при бързо търсене.
Дървета с балансирана височина
В най-лошия случай, когато дървото е изродено в линеен списък, съхраняването на данни в подредено двоично дърво не дава никаква печалба в сложността на операциите в сравнение с масив или линеен списък. В най-добрия случай, когато дървото е балансирано, всички операции имат логаритмична сложност, което е много по-добре.Перфектно балансираное дърво, което за всеки връх отговаря на изискването: броят на върховете в лявото и дясното поддървета се различава с не повече от 1.
Перфектният баланс обаче се поддържа доста трудно. В някои случаи добавянето или премахването на елементи може да изисква значително повторно изграждане на дървото, което не гарантира логаритмична сложност. През 1962 г. двама съветски математици: G.M. Аделсон-Велски и Е.М. Ландис въвежда по-малко строга дефиниция на баланса и доказа, че с такава дефиниция е възможно да се пишат програми за добавяне и/или изтриване, които имат логаритмична сложност и поддържат дървото балансирано. Едно дърво еABL-балансирано(съкратено от имената на G.M. Adelson-Velsky и E.M. Landis), ако за всеки връх е изпълнено следното изискване: височините на лявото и дясното поддървета се различават с не повече от 1. Не всяко AVL-балансирано дърво е идеално балансирано, но всяко перфектно балансирано дърво е AVL-балансирано.
Операциите за добавяне и премахване може да нарушатбаланс на дървото. В този случай са необходими някои трансформации, които не нарушават реда на дървото и допринасят за по-добър баланс.
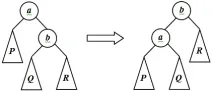
Нека разгледаме такива трансформации. Нека връх a има дясно дете b . Означаваме с P лявото поддърво на върха a , с Q и R съответно лявото и дясното поддърво на върха b. Подреждането на едно дърво изисква P. По същия начин, подреждането на дърво с корен b , лявото му дете a , в което P и Q са лявото и дясното поддърво на a , R е дясното поддърво на b , изисква същото. Следователно първото дърво може да се трансформира във второто, без да се нарушава редът. Такава трансформация се наричамалка дясна ротация(фиг. 40.3).Малкото ляво завъртане, симетрично на него, се определя по подобен начин.
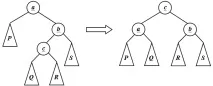
Нека b е дясното дете на възел a, c лявото дете на възел b, P лявото поддърво на възел a, Q и R съответно лявото и дясното поддърво на c, S дясното поддърво на b. Тогава P. Същият ред съответства на дърво с корен c, имащо ляво дете a и дясно дете b, за които P и Q са поддървета на a, а R и S са поддървета на b. Съответната трансформация ще се наричаголямо дясно завъртане(фиг. 40.4).Голямото ляво завъртане, симетрично на него, се определя по подобен начин.
Схематичноалгоритъмът за добавяне на нов елемент към AVL-балансирано дървоще се състои от следните три основни стъпки.
Стъпка 1. Търсене на дърво.
Стъпка 2. Вмъкване на елемента на мястото, където е приключило търсенето, ако елементът липсва.
Стъпка 3. Ребалансирайте.
Първата стъпка е да се уверите, че елементът не съществува в дървото, а също и да намерите точка на вмъкване, така чеслед вмъкването дървото остана подредено. Третата стъпка е преминаване назад по пътя на търсене: от точката на добавяне до корена на дървото. Докато се движите по този път, индикаторите за баланс на преминатите върхове се коригират и се извършва балансиране, където е необходимо. Добавянето на елемент към дърво никога не изисква повече от едно завъртане.
Алгоритъмът за премахване на елемент от балансирано дървоще изглежда така:
Стъпка 1. Търсене на дърво.
Стъпка 2. Премахване на елемент от дървото.
Стъпка 3. Ребалансиране на дървото (обратен проход).
Първата стъпка е да намерите възела в дървото, който трябва да бъде премахнат. Третата стъпка е връщане от мястото, откъдето е взет елементът, за да замени премахнатия, или от мястото, откъдето е премахнат елементът, ако замяната не е била необходима. Операцията за изтриване може да изисква повторно балансиране на всички върхове по пътя обратно към корена на дървото, т.е. от ред log n върха. По този начин алгоритмите за намиране, добавяне и премахване на елементи в AVL-балансирано дърво имат сложност, пропорционална на O(log n).
Цифрови (побитови) дървета за търсене
Методите за цифрово търсене са доста тромави и зле илюстрирани. Помислете за двоично цифрово дърво за търсене. Както в дърветата, обсъдени по-горе, във всеки връх на такова дърво се съхранява пълният ключ, но преходът по левия или десния клон се извършва не чрез сравняване на референтния ключ със стойността на ключа, съхранен във върха, а въз основа на стойността на следващия бит от аргумента. Цифровото търсене се осъществява бит по бит (бит по бит).
Търсенето започва от корена на дървото. Ако ключът, съдържащ се в основния възел, не съответства на аргумента за търсене, тогава най-левият бит се анализира.аргумент. Ако е равно на 0, преходът се извършва на левия клон, ако 1 - на десния. Ако ключът не съвпада с аргумента за търсене, тогава следващият бит от аргумента се анализира и т.н. Търсенето приключва, когато всички битове на аргумента са проверени или се срещне връх с липсваща лява или дясна препратка.
Ключови термини
Двоично цифрово дърво за търсенее дърво, всеки връх на което съхранява пълния ключ и преходът през клоновете се извършва въз основа на стойността на следващия бит от аргумента.
Двоично (двоично) дървое йерархична структура, в която всеки възел има не повече от две деца.
Перфектно балансирано дървое дърво, което отговаря на изискването за всеки връх: броят на върховете в лявото и дясното поддървета се различава с не повече от 1.
Ключ за търсенее полето, чиято стойност се използва за търсене на .
Оптималното двоично дърво за търсенее двоично дърво за търсене, изградено, за да осигури максимална производителност за дадено вероятностно разпределение за търсене на необходимите данни.
Търсенетое процес на намиране на специфична информация в предварително създаден набор от данни.
AVL-балансирано дървое дърво, за всеки връх на което е изпълнено изискването: височината на лявото и дясното поддървета се различават с не повече от 1.
Дървета за произволно търсенеса подредени двоични дървета за търсене, където елементите се вмъкват в произволен ред, когато са създадени.
Подреденото двоично дървое двоично дърво, в което за всеки от неговите върхове x свойствата са верни: всички елементи в лявото поддърво са по-малки от елемента, съхранен в x; всички елементи в дясното поддърво са по-големиелемент, съхраняван в x; всички елементи на дървото са различни.
Частично подредено двоично дърво е подредено двоично дърво, в което се срещат едни и същи елементи.