KNOW INTUIT, Лекция, Комбинирани микросхеми
Чиповете Adder (английски Adder), както подсказва името им, са предназначени да добавят два входни двоични кода, тоест изходният код ще бъде равен на аритметичната сума на двата входни кода. Например, ако един входен код е 7 (0111), а другият е 5 (0101), тогава общият изходен код ще бъде 12 (1100). Сумата от две двоични числа с брой цифри N може да има брой цифри (N + 1). Например, събирането на числата 13 (1101) и 6 (0110) води до числото 19 (10011). Следователно броят на изходите на суматора е с един повече от броя на цифрите на входните кодове. Този допълнителен (най-значим) бит се нарича пренасящ изход.
На диаграмите суматорите се означават с буквите SM. В домашните серии кодът, обозначаващ чипа на суматора, е IM.
Суматорите са еднобитови (за сумиране на две едноцифрени числа), 2-битови (събиране на 2-битови числа) и 4-битови (събиране на 4-битови числа). Най-често се използват 4-битови суматори. На фиг. 6.1 показва например 2-битови и 4-битови суматори. Чипът IM6 се различава от IM3 само с повишена скорост и броя на използваните щифтове на микросхемата, функцията е същата.
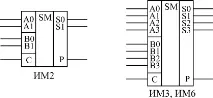
Освен изходните битове на сумата и изхода на трансфера, суматорите имат вход за разширение (друго име е вход за трансфер) C за комбиниране на няколко суматора с цел увеличаване на капацитета. Ако единица дойде на този вход, тогава изходната сума се увеличава с единица, ако дойде нула, тогава изходната сума не се увеличава. Ако се използва един разширителен чип, тогава трябва да се приложи нула към неговия разширителен вход C.
Например в табл. 6.1 показва пълната таблица на истинността на 2-битовия суматор IM2. какот таблицата се вижда, че изходният 3-битов код (P, S1, S0) е равен на сумата от входните 2-битови кодове (A1, A0) и (B1, B0), както и на сигнала C. Нулевите битове са по-ниски, първите битове са по-високи. Пълната таблица на истината на 4-битов суматор би била прекалено голяма, така че не е дадена. Но същността на работата остава точно същата като в случая на 2-битов суматор.
Суматорите могат да се използват и за сумиране на числа в отрицателна логика (когато логическа единица съответства на електрическа нула и обратното, електрическа единица съответства на логическа нула). Но в този случай пренасящият входен сигнал C също става обърнат, така че когато се използва един чип на суматора, към входа C трябва да се приложи електрическа единица (ниво на високо напрежение). Изходният сигнал за трансфер P също става обратен, ниското ниво на напрежение върху него (електрическа нула) съответства на наличието на трансфер. Тоест, оказва се, че суматорът работи по абсолютно същия начин както с положителна, така и с отрицателна логика.
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
Помислете за пример. Да предположим, че трябва да съберем две числа 5 и 7 в отрицателна логика. Числото 5 в положителната логика съответства на двоичен код 0101, а в отрицателната логика - код 1010. Числото 7 в положителната логика съответства на двоичен код 0111, а в отрицателната логика - код 1000. Когато кодовете 1010 (десетично число 10 в положителната логика) и 1000 (десетично число 8 в положителната логика) се подадат на входа на суматора, получаваме сума 1 0 + 8 = 18, т.е. код 10010 в положителна логика. При входен пренасящ сигнал С=1 (няма входен пренос при отрицателна логика), изходният код на суматора ще бъде още един: 18 + 1 = 19, т.е. 10011. С отрицателенЛогично, това ще съответства на числото 01100, тоест 12 при липса на изходно пренасяне. Резултатът е 5+7=12.
Суматорът може да изчислява не само сумата, но и разликата на входните кодове, тоест може да работи като изваждане. За да направите това, числото, което трябва да се извади, трябва просто да бъде обърнато побитово и към входа за прехвърляне C трябва да бъде подаден единичен сигнал (фиг. 6.2).
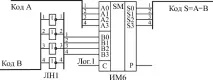
Например, да кажем, че трябва да изчислим разликата между числото 11 (1011) и числото 5 (0101). Обръщаме числото 5 бит по бит и получаваме 1010, тоест десетично 10. Суматорът, когато сумира 11 и 10, ще даде 21, тоест двоичното число 10101. Ако сигналът C е 1, тогава резултатът ще бъде 10110. Изхвърляме най-значимия бит (изходен сигнал P) и получаваме разликата 0110, тоест 6.
Друг пример. Нека е необходимо да се изчисли разликата между числото 12 (1100) и числото 9 (1001). Обръщаме 9 бит по бит, получаваме 0110, тоест десетично 6. Намираме сумата от 12 и 6, получаваме 18 и като вземем предвид C \u003d 1, получаваме 19, тоест двоично 10011. В четирите най-малко значими цифри имаме 0011, тоест десетично 3.
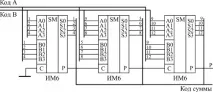
Каскадните суматори за увеличаване на битовата дълбочина са много прости. Необходимо е да се подаде сигнал от трансферния изход на суматора, който обработва по-ниските битове, към трансферния вход на суматора, който обработва по-високите битове (фиг. 6.3). Когато се комбинират три 4-битови суматора, се получава 12-битов суматор, който има допълнителен 13-ти бит (пренасящ изход P).
Несигурни състояния на изходите на суматора могат да възникнат при всяка промяна в някой от входните кодове (фиг. 6.4). Изходният код на сумата може да поеме за кратко време стойности, които по никакъв начин не са свързани с входните кодове, а на изхода на трансфера могат да се появят кратки фалшиви импулси. Това се дължи главно на неедновременната промяна на битовете на входакодове. За да се избегне влиянието на тези несигурни състояния върху по-нататъшната верига, е необходимо да се осигури синхронизация или стробиране на изходните сигнали. Но за това е необходимо да имате информация за моментите на промяна на входните кодове, която далеч не винаги е налична.
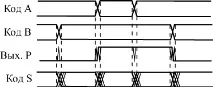
Закъсненията на суматора IM6 от входовете към изходите на сумата са приблизително два пъти по-големи от закъснението на логическия елемент, а от входовете към изхода за прехвърляне - приблизително един път и половина. Закъсненията на суматора IM3 са почти два пъти по-големи от закъсненията на IM6. Следователно, във вериги, където скоростта е важна, е по-добре да използвате IM6. Това е особено важно при каскадиране за увеличаване на битовата дълбочина, тъй като там се сумират закъсненията на отделните микросхеми. Точните стойности на закъсненията трябва да се търсят в справочници.