Код на Хеминг (7; 4)
Здравейте всички! Днес искам да ви разкажа малко за кода на Хеминг (7; 4). Този най-прост код може лесно да се използва от всеки за изпращане на самокоригиращи се съобщения и днес искам да ви покажа как точно този код може да се използва лесно и просто.
Структурно думите на кода на Хеминг се състоят от две части. Първо има 4 информационни бита, след това три тестови бита. Ще обозначим информационните битове с буквите ABCD, проверката с буквите xyz.
Така кодовата дума на Хеминг има следната структура:
За да предадем 4 бита информация, трябва да предадем кодова дума от цели 7 бита! Последните три бита в случай, че няма грешки, не носят никаква нова информация, защото зависят от първите 4. Въпреки това, ако се появи 1 грешка в кодова дума от 7 бита, тогава оригиналните информационни 4 бита все още могат да бъдат възстановени точно! Това е основната характеристика на самокоригиращите се кодове.
Естествено, използването на кода на Хеминг за предаване на данни изисква повече ресурси. Тук има толкова важна концепция като скоростта на кода - съотношението на броя на информационните битове към общия брой битове. В случая на кода на Хеминг процентът е 4/7. Тоест, например, за предаване на информация със скорост 1 Mbps и коригиране на грешки с помощта на кода на Hamming, ви е необходим канал с честотна лента поне 7/4=1,75 Mbps.
Следните формули могат да се използват за преброяване на контролните битове:
x = A + B + C mod 2,
y = A + B + D mod 2,
z = A + C + D mod 2,
където n mod 2 означава остатъка от деленето на числото n на 2.
Например, ако информационният вектор е ABCD = 1001, тогава кодовият вектор ще бъде ABCDxyz = 1001 100
Вместо неразбираеми формули можете да използвате следнотоснимка:
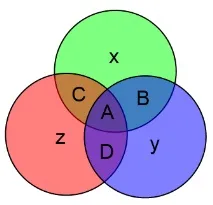
Тук всичко е много просто. Заменете стойностите на съответните битове вместо букви и след това изчислете стойностите на x, y и z като сумата по модул 2 на тези информационни битове, които са в съответния кръг.
Примерът по-горе би бил:
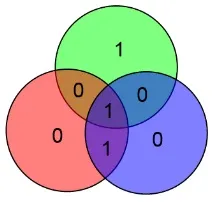
Много по-интересен е въпросът за коригиране на грешки. Очевидно получателят може да заключи, че няма грешки, просто като вземе информационните битове ABCD, изчисли контролните битове xyz на тяхна база и сравни изчислените контролни битове с получените. Ако има грешка, част от контролните битове няма да съвпадат.
Да предположим, че е възникнала грешка в контролния бит y и е получена дума 1001 110
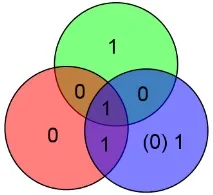
В този случай два контролни бита ще се сближат, но един не. Това е напълно достатъчно, за да заключим, че битът y (за който проверката не се сближи) трябва да бъде коригиран.
Да предположим, че е възникнала грешка в един от информационните битове на BCD - например в бит B.
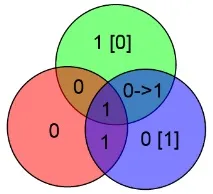
В този случай до два бита за проверка - x (той е равен на 1 и "трябва" да е равен на 0) и y няма да се сближат. Гледайки кръговете, можем лесно да видим, че те се пресичат в битове B и A. две проверки не се сближиха, тогава вземаме бит B (разположен в пресечната точка на две проверки).
И накрая, разгледайте отделно бит А. Ако има грешка в него, тогава и трите проверки няма да се сближат:
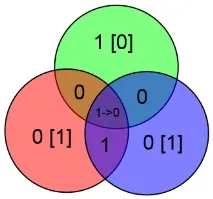
Виждайки такъв позор, веднага заключаваме, че грешката е в бит А.
По този начин е лесно и просто да се изчисли местоположението на грешката и да се коригира. Отбелязвам, че ако има повече от една грешка, тогава описаният по-горе алгоритъм ще работи неправилно. Да предположим например, че има грешки в C и z битовете:
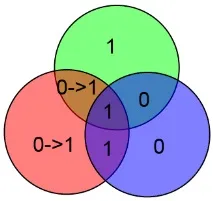
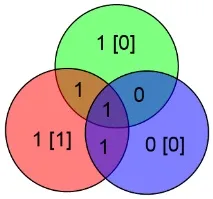
Битовете за проверка y и z ще се сближат, но битът x не. Алгоритъмът ще коригира бит х и това е всичко. Доста еестествено поведение, т.к. ако вероятността за грешка p 0).
Естествено, работата с цветни кръгове е удобна за човек, но неудобна за компютър. Кодовете на Хеминг имат една функция, която им позволява лесно да бъдат декодирани на компютър. Така че, помислете за следния алгоритъм:
Нека дефинираме числата g, b, r като сбор от четирите бита в кръгове от съответния цвят. Тези.:
g = A + B + C + x mod 2,
b = A + B + D + y mod 2,
r = A + C + D + z mod 2.
Всъщност всеки от тези битове може да се дефинира като сбор от съответния контролен бит, изчислен от получените информационни битове с получения контролен бит. Тези. например g е сумата от (A + B + C mod 2) (според тази формула x се разглежда от страната на предавателя) и полученото x. По същия начин, b съответства на y, r съответства на z.
Ако няма грешки, тогава gbr = 000 (получените битове за четност се сближават с тези, изчислени на базата на информационния вектор).
Ако има 1 грешка, тогава числото gbr е числото (в двоичен запис) на грешния бит във вектора ABCxDyz.
Като пример, разгледайте вече познатия вектор ABCDxyz = 1001 100, в който възникна грешка в бит x (четвъртият бит във вектора ABCxDyz). Нека изчислим gbr:
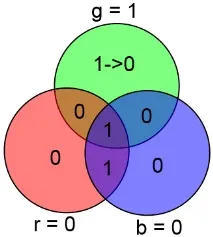
gbr = 100 [2] = 4 [10]. Грешка в бит 4, който е x. По този начин, за да се декодира и коригира грешка в кодова дума с дължина 7, е необходимо само да се изчислят три суми и с помощта на проста функция да се получи местоположението на грешката от полученото число.