Комбинирано вземане на проби
Комбинираното вземане на проби включва използването на няколко метода за вземане на проби. Можете да комбинирате, например, серийно вземане на проби и произволно вземане на проби. В този случай, чрез разделяне на генералната съвкупност на серии (групи) и избор на необходимия брой серии, се получава произволна извадка от единици в серията. Такова комбинирано вземане на проби може да бъде многократно (за групи и единици) и еднократно.
Средната грешка на комбинираната проба се определя по формулите (символите са дадени по-рано):
При повторен избор,
С неповтаряща се селекция -
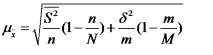
Многоетапно вземане на проби
Многоетапното вземане на проби включва извличане от генералната съвкупност, първо на разширени групи единици, след това групи с по-малки размери и така нататък, докато не бъдат избрани онези групи (серии) или отделни единици, които ще бъдат подложени на наблюдение. Извадката може да бъде двуетапна, когато генералната съвкупност се разделя на групи и се избират групите, след което в рамките на групите се извършва избор на единици за наблюдение. И на двата етапа изборът може да се извърши на случаен принцип.
За разлика от типичната селекция, при която селекцията се извършва от всички групи без изключение, при многоетапна селекция се избират самите групи и следователно не всички попадат в извадката.
Броят на етапите на подбор може да бъде повече от два. Ако броят на етапите на подбор е повече от два, тогава средната грешка на извадката се определя по формулата
µ =
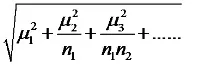
където µ1, µ2, µ3, …….- средни грешки при вземане на проби при отделни стъпки за избор,
n1, n2, ……. - броя на пробите на съответните стъпки.
Многофазово вземане на проби
При многофазното вземане на проби, рамките за вземане на проби се формират по такъв начин, че част от информацията се събира от всички единици за вземане на проби, след което се избират още някои.единици, които се разглеждат по по-широка програма. Грешката на многофазната извадка се изчислява за всяка фаза поотделно.
Малки мостри
Извадки, в които наблюдението обхваща малък брой единици (n 2 е дисперсията на малка извадка:
,
къдетохр. е средната стойност на характеристиката в извадката,
n-1 - брой степени на свобода (n -1 = k),
t е доверителният коефициент на малка извадка, който зависи не само от дадената доверителна вероятност, но и отброяизвадкови единици.
Вероятността общата средна стойност да е в определени граници се определя по формулата
,
За да се изчисли коефициентът на доверие t, стойността на функцията S(t) се определя по формулата
където P е стойността на доверителната вероятност.
След това, споредтаблицата за разпределение на Стюдънт(вижте статистическите таблици), в зависимост от стойността на функцията S(t) и броя на степените на свобода k (k = n-1), се определя стойността на t.
Функцията S(t) също се използва за определяне на вероятностите, че действителното нормализирано отклонение
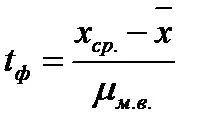
Вероятността действителното съотношение (tf) да не надвишава табличната стойност (t) по абсолютна стойност се определя по формулата
.
Вероятността действителното съотношение (tf) да надвиши табличната стойност (t) по абсолютна стойност се определя по формулата
.
Пример. 5.
Беше направенамалкапроба от партида електрически лампи (случаен избор, неповтарящи се), за да се определи продължителността на експлоатационния живот на лампите. Резултатите от пробата са дадени в табл. 4.8.