Конвейерна обработка на данни

Обикновените аритметични операции се поддават лесно на конвейер. Нека да разгледаме няколко примера.

Тръбопроводен целочислен суматор

Сумирането на цели числа се основава на сумирането на една двоична цифра (фиг. 1).

Нека представим операцията в следния вид (фиг. 2).

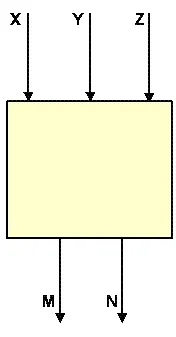Тук и са стойностите на съответната цифра в първия и втория член, е прехвърлянето от най-малката цифра, е стойността в разглежданата цифра след добавяне, е стойността на прехвърлянето към най-значимата цифра.

Въпросната операция може да бъде представена с таблица:

С помощта на този алгоритъм може лесно да се изгради класически суматор на цели числа с последователно пренасяне (фиг. 3).

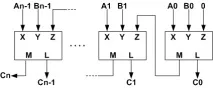Този суматор изпълнява операция.

В този суматор сумирането на цифрите се извършва последователно, тъй като за да се сумира всяка следваща цифра, е необходимо да се знае пренасящият бит, получен чрез сумиране на предишната цифра. Ако времето за сумиране на всеки бит е , тогава общото време за сумиране на двубитовите числа е

Същият суматор в конвейерната версия изглежда така (фиг. 4):

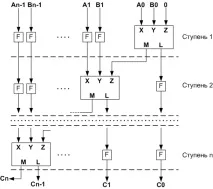Както се вижда от фиг. 4, на всяка стъпка от тръбопровода се сумира един бит. Останалите цифри остават непроменени и се съхраняват в специални ключалки. Такъв конвейер позволява сумирането на поток от цели числа - докато вторият бит от първата двойка числа се добавя, сумирането на първия бит от втората двойка числа може вече да започне. Важно е да се отбележи, че времето за сумиранеедин чифт не се променя - остава равен. Но интервалът на спускане на резултатите от суматора вече е равен не на , както преди, а на . Тоест, при сумиране на потока от данни конвейерният суматор е няколко пъти по-бърз.

Суматор с плаваща запетая на тръбопровода

Във формат с плаваща запетая, представянето на число се състои от два компонента - експонента и мантиса (фиг. 5).

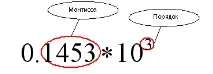В изчислителните системи числата с плаваща запетая винаги се представят в нормализирана форма - винаги има различна от нула цифра след точката. Това ви позволява да се отървете от неяснотата на представянето в този формат. Тъй като винаги има нула вляво от точката, тя не се съхранява в паметта на компютъра, както самата точка. Представянето на число във формат с плаваща запетая в компютър има формата (фиг. 6):

Определен брой цифри се отделят за представяне на число (минимум 32). Най-значимата цифра кодира знака на числото, след това се намира мантисата, а след нея експонентата, също със знак.

За да добавите две числа с плаваща запетая, изразени в нормализирана форма, трябва:

Подравнете поръчките според по-голямото от числата, като "изместите" мантисата на по-малкото число надясно със съответния брой цифри.
Тъй като получените числа имат еднакъв ред, събирането им се свежда до събиране на мантисата като обикновени цели числа (мантисата е цяло число).
След добавянето е необходимо получената сума да се представи в нормализирана форма, като се коригира мантисата и реда.

Конвейерен суматор, работещ съгласно този алгоритъм, е показан на фиг. 7.

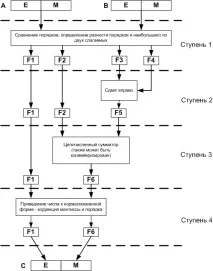И така, входът на конвейера получава две числа във формат с плаваща запетая.запетая ( и ).

На първия етап от конвейера поръчките се сравняват и се определя максималното от двете числа, както и разликата в поръчките. На изхода междинните стойности се фиксират във фиксаторите: F1 е най-високият ред, F2 е мантисата на числото с най-висок ред, F3 е мантисата на числото с най-нисък ред, F4 е разликата в поръчките.

На втория етап от конвейера числата се привеждат в същия ред чрез изместване на мантисата на по-малкото число надясно. На изхода междинните стойности се фиксират във фиксаторите: F1 е редът (сега е еднакъв и за двете числа), F2 е мантисата на първия член, F5 е мантисата на втория член.

На третия етап се извършва целочисленото сумиране на мантисите. Суматорът за цели числа, използван в този случай, може от своя страна да бъде конвейерен. На изхода имаме F1 - редът на сумата, F6 - мантисата на сумата.

На четвъртия етап получената сума се редуцира до нормализирана форма с корекция на мантисата и реда. На изхода: F1 е редът на сумата след редукция до нормализирана форма, F6 е мантисата на сумата след редукция до нормализирана форма. Резултатът е число с плаваща запетая, което ще бъде сумата от оригиналните числа и .