Корен на дърво
Производствен процес на фотомаска
Със защита със слой маска
Дъщерни върхове
Полученият набор от върхове се анализира за наличието на целевия връх, т.е. връх, който няма дъщерни върхове. Процедурата продължава, докато се намери целевият връх. В предишната фигура целевите пикове са ABDK и ABDL - пикове от 4-то ниво.
Търсенето на решения е итеративно по природа и броят на итерациите и върховете, отворени преди намиране на целевото състояние, зависи значително от реда, в който върховете са отворени. Редът, в който се разкриват върховете, се нарича СТРАТЕГИЯ ЗА ТЪРСЕНЕ.
Могат да се разграничат два основни типа стратегии за търсене (фиг. 6.4):
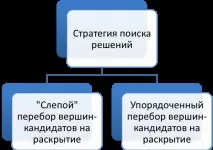
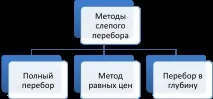
Сляпото изброяване се характеризира с факта, че местоположението на целевите върхове и тяхната близост не влияят на реда на разширяване. Има няколко метода за сляпо изброяване, показани на фигура 6.5.
За структуриран запис на методи за намиране на решения в пространството на състоянието, ние въвеждаме концепциите за отворени списъци с върхове (OTC) и списъци с затворени върхове (CLL). Списъкът със затворени върхове е списък, който съдържа идентификаторите на отворените върхове и идентификатора на върха, който трябва да бъде отворен в момента. Върховете от списъка ZKR, с изключение на последния, не могат да бъдат отворени. Списъкът с отворени върхове е списък с върхове, които могат и трябва да бъдат отворени. Стратегиите за търсене или вземане на решения се различават по правилата за поставяне на върхове в OTK списъка и избор на следващия връх за разкриване.
1. Метод на изчерпателното изброяване.
Тук върховете се разширяват в реда, в който са били генерирани.
Алгоритъмът, който прилага този метод, може да бъде представен по следния начин:
1.1. Поставете началния връх в OTK списъка.
1.2. Ако OTC списъкът е празен, дайте сигналнеуспешно търсене, в противен случай преминете към следващата стъпка.
1.3. Вземете първия връх от списъка OTK и го прехвърлете в списъка ZKR. Дайте на върха ID на V.
1.4. Разширете връх V. Поставете всички дъщерни върхове, които не са намерени в списъка ZKR, в края на OTC списъка и изградете указатели, водещи от тях до връх V. Ако връх V няма дъщерни върхове, тогава преминете към стъпка 1.2.
1.5. Проверете дали един от дъщерните върхове на V е целта. Ако е така, издайте решение; в противен случай преминете към стъпка 1.2.
Този алгоритъм предполага, че началният връх не отговаря на поставената цел, въпреки че не е трудно да се въведе стъпка за проверка за такава възможност. Върховете и указателите, изградени по време на итерацията, образуват поддърво на цялото имплицитно дефинирано дърво на пространството на състоянието. Ще наричаме такова поддърво изброяващо дърво.
Методът на груба сила със сигурност ще намери най-краткия път до целевия връх, при условие че такъв път изобщо съществува. (Ако няма такъв път, тогава посоченият метод ще обяви неуспех в случай на крайни графики, а в случай на безкрайни графики, алгоритъмът никога няма да завърши работата си.)
2. Метод на равните цени.
Възможно е да има задачи, при които към решението са наложени други изисквания, различни от изискването за получаване на най-кратката последователност от оператори. Присвояването на конкретни цени на дървовидните дъги (и след това намирането на пътя за вземане на решение с най-ниска цена) изпълнява много от тези обещани критерии. По-обща версия на метода за изчерпателно търсене, нареченметод на равна цена, позволява във всички случаи да се намери някакъв път от началния връх до целевия връх, чиято цена е минимална. Докато в горния алгоритъмразпространява линии с еднаква дължина на пътя от началния връх, в по-общ алгоритъм, който ще бъде описан по-долу, се разпространяват линии с еднаква цена на пътя.
Нека всяка дъга е свързана с някаква функция на разходите CIJ. Същността на метода е да се намери пътя с минимални разходи. В противен случай преминете към следващата стъпка. Върховете се разкриват във възходящ ред на тяхната цена. Ако означим с G(v) цената на отваряне на определен връх v, тогава алгоритъмът, който прилага този метод, може да бъде представен по следния начин:
2.1. Поставете началния връх S0 в OTC списъка. Поставете G(S0)=0.
2.2. Ако OTC списъкът е празен, сигнализирайте за неуспешно търсене; в противен случай преминете към следващата стъпка.
2.3. Вземете от OTC списъка върха, за който стойността на G(v) има най-малка стойност, и го поставете в ZKR списъка. Присвоете идентификатора v на този връх.
2.4. Ако v е целевият връх, тогава връща пътя на решението;
2.5. Отворен връх v. За всеки дъщерен възел vi изчислете цената G(vi), като използвате формулата G(vi)=G(v)+C(v,vi). Поставете тези върхове заедно със съответните им G(vi) в OTK списъка и конструирайте указатели, преминаващи от тях към върха v. Ако връх v няма дъщерни върхове, веднага преминете към стъпка 2.
2.6. Отидете на стъпка 2.
Алгоритъмът за равна цена може също да се използва за намиране на пътища с минимална дължина чрез просто задаване на цената на всяко ребро наедно. Ако има няколко начални върха, алгоритъмът просто се променя: в стъпка (1) всички начални върха се поставят в списъка OPEN. Ако състоянията, съответстващи на поставената цел, могат да бъдат описани изрично, тогава процесът на изброяване може да започне в обратна посока, като целевите върхове се приемат катопървоначално и използвайки инверсията на оператора G.
3. Метод на търсене в дълбочина.
Ако дефинираме дълбочината на върха с число, равно на номера на неговото ниво, тогава при използване на метода търсене в дълбочина винаги се разкрива този от върховете, който има най-голяма дълбочина. Тъй като няколко върха могат да имат еднаква максимална дълбочина, се предполага, че има правило за избор на един от тях. Тези. дълбочината на границата е зададена. Върховете с дълбочина, равна на дълбочината на границата, не се разширяват. По този начин методът за търсене в дълбочина може да се дефинира като метод за търсене, при който се разкрива един от върховете, който има най-голяма дълбочина, по-малка от граничната.
Този подход може да доведе до разгръщане на процеса по някакъв безполезен път, така че трябва да се въведе някаква процедура за връщане. След като процесът изгради връх с дълбочина, която надвишава някаква дълбочина на границата, ние разкриваме върховете с най-голяма дълбочина, която не надхвърля тази граница, и т.н.
Алгоритъмът, който прилага метода за търсене в дълбочина, може да бъде представен по следния начин:
3.1. Поставете началния връх в OTK списъка.
3.2. Ако OTK списъкът е празен, издайте съобщение за неуспешно търсене, в противен случай преминете към стъпка 3.
3.3. Вземете първия връх от списъка OTK и го прехвърлете в списъка ZKR. Присвоете идентификатора v на този връх.
3.4. Ако дълбочината на върха v е равна на дълбочината на границата, тогава преминете към стъпка 2, в противен случай отидете към стъпка 5.
3.5. Отворен връх v. Поставете всички дъщерни върхове в началото на OTC списъка и изградете указатели, преминаващи от тях към връх v. Ако v няма деца, преминете към стъпка 2.
Алгоритъмът за първо търсене в дълбочина първо итерира по един път, докато се достигне максималната дълбочина, след товаразглеждат се алтернативни пътеки със същата или по-малка дълбочина, които се различават от него само с последната стъпка, след което се разглеждат пътеките, маркирани от последните две стъпки и т.н.
Във всички разглеждани методи за изброяване се приема, че има само един начален връх.
2. Методи за подредено изброяване.
За повечето практически проблеми е възможно да се формулират емпирични правила, които позволяват да се намали количеството на изброяването. Тези правила използват специфична информация за решавания проблем, формирана на базата на опит, интуиция и здрав разум на експерт и инженер по знания.
Информация от този вид се нарича евристична, а методите и алгоритмите, базирани на нея, се наричат евристични. Основната идея на евристичните методи е да се подреди списъкът с отворени върхове според някаква мярка, която оценява "обещаващото" на върха или пътя, на който се намира дадения връх.
Такава мярка се нарича ФУНКЦИЯ ЗА ОЦЕНКА, а процедурите от този тип се наричат подредени методи за изброяване. За следващото разкриване върхът, който има минималната стойност на функцията за оценка, се избира от списъка OTK. След всяка стъпка на разширяване върховете в списъка се пренареждат според стойностите на функцията за оценка.
Като функции за оценка можете да изберете функциите, показани на Фигура 6.6.
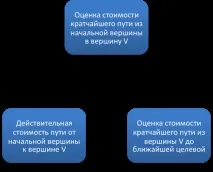
Няма конструктивни препоръки как да се дефинират функциите за оценка. Разгледайте значението му с пример (фиг. 6.7)
Например, помислете за местоположението на кубчетата на сайтовете