Критерий за устойчивост на Михайлов
Нека вземем характеристичния полином на линейната системаn-ти ред
с положителни коефициенти (необходимо условие за устойчивост). Заместване в него на чисто въображаема стойност=j; получаваме
,
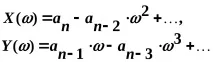
На практика ходографът се изгражда по точки. Няколко различни стойностиса зададени в интервала между0и(една точка във всеки квадрант е достатъчна) и координатите на точките от кривата на МихайловX(),Y().
Тези ходографи се наричат криви на Михайлов. Те имат за различниnприблизително същите форми, както е показано на фигурата.
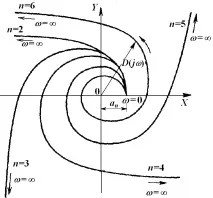
Граничните стойности+или–зависят от показателяn.
Дефиниция на критерия Михайлов
За стабилносттана линейна система отnпорядъке необходимоидостатъчно,кривата на Михайлов да преминава последователноnквадранта обратно на часовниковата стрелка (през цялото време около началото).
Определяне на границите на устойчивост по критерия Михайлов.
Графично това означава, че една точка от кривата на Михайлов=0попада в началото на координатите, както е показано на фигурите:
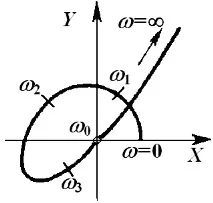
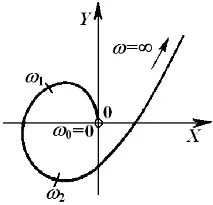
Физическият смисъл на величината=0е честотата на трептене на системата на границата на устойчивост.
На границата на стабилност на системата всички други корени, с изключение на=j0, трябва да лежат отляво на въображаемата ос на равнината. В противен случай системата ще бъде нестабилна. Ето защоизисква се кривата на Михайлов да преминава през всички други квадранти, с изключение на пропуснатия поради преминаване през началото, както е показано например заn=5, на фиг. b.
Следователно, например, ходографът на следващата фигура не съответства на границата на устойчивост, а на нестабилна система.
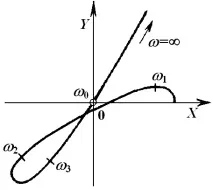
Изразите заXиYсе използват законструиране на областите на стабилностна системата в равнината на всеки два параметъраAиB, избрани по време на проектирането на системата (например усилване и времева константа).
На границата на стабилност имаме:
освен това параметритеAиBса включени в коефициентите на характеристичното уравнение на системата. Чрез посочване на различни стойности за0(0), стойностите на параметритеAиBсе определят от тези уравнения. В резултат на това границите на устойчивост на равнинатаA,Bса построени от точки.
Пример.Разгледайте определянето на границите и зоната на стабилност на системата според критерия на Михайлов за прост случай. Нека характеристичното уравнение е:
, .
Според критерия на Михайлов е удобно да се определят регионите на стабилност за системи от всякакъв ред. Предимството на критерия на Михайлов е, че той е по-прост и по-ясен за определяне на стабилността на система от критерия на Хурвиц, особено за системи от висок ред.