кубично тяло
Лекция 19
Основните определения и твърдения на тази лекция са подобни на съответните дефиниции и твърдения на Лекция 17. Това ни позволява да се ограничим до основните формулировки.
19.1. Концепцията за кубично тяло
"- околността на точка А в триизмерното пространство, ще наричаме множеството от всички онези точки в пространството, които се намират вътре в топката с радиус " с център в точка А.
Точка A се нарича вътрешна точка на произволен набор T от точки в пространството, ако има "> 0, така че "-околността на точка A принадлежи изцяло на множеството T.
Точка A се нарича гранична точка на произволно множество T от точки в пространството, ако във всяка "-околност на точка A има както точки, принадлежащи на множеството T, така и не принадлежащи на T. Множеството от всички гранични точки на множеството се нарича
Xia е границата на това множество.
Множество от точки в триизмерното пространство се нарича ограничено, ако съществува топка, съдържаща всички точки от това множество.
Тялото T ще се нарича всяко ограничено множество от точки в триизмерно пространство
Сред всички тела ние отделяме така наречените полиедри (по-точно триизмерни полиедри) тела, чиято граница е съвкупност от краен брой
равнинни полигони в тримерно евклидово пространство (фиг. 1), така че:
1. всяка страна на който и да е от многоъгълниците е същевременно страната на другата (но само една), наречена съседна на първата (по тази страна);
2. от който и да е от многоъгълниците, които съставляват полиедъра, можете да стигнете до който и да е от тях, като отидете до този, който е съседен на него, и от това дообърнете се към съседния и т.н.
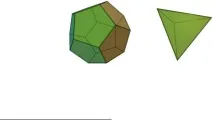
Ориз. 1: Полиедри: додекаедър, тетраедър.
Тези многоъгълници се наричат лица, техните страни са p ¼ bram, а върховете им са върховете на многостена.
Обемът на всеки полиедър може да се намери, като се раздели на непресичащи се тетраедри 1 (без общи вътрешни точки) (фиг. 2). От курса на гимназията, осн
1 Тетраедърът е най-простият многостен, чиито лица са четири триъгълника.