L7 - Метод на резолюции

Лек.7.Логично следване. логично заключение.

Метод на резолюциите в логиката на предикатите от първи ред.

Логиката от първи ред, като формализиран аналог на обикновената логика, дава възможност да се разсъждава строго относно истинността и неистинността на твърденията и тяхната взаимовръзка, по-специално относно логическото следствие на едно твърдение от друго или, например, относно тяхната еквивалентност.

Помислете за класически пример за формализиране на изрази на естествен език в логиката от първи ред. Нека вземем аргумента: "Всеки човек е смъртен. Конфуций е човек. Следователно Конфуций е смъртен." Означават:

"x е човек" - чрезMAN(x),

Тогава твърдението "всеки човек е смъртен" може да бъде представено с формулата:

(

)(ЧОВЕК(x) → СМЪРТ(x)).

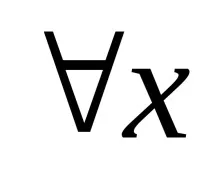
И твърдението "Конфуций е човек" - формулата:

и "Конфуций е смъртен" - по формулата:

Изявлението като цяло вече може да бъде написано като:

(

)(ЧОВЕК(x) → СМЪРТ(x)) & ЧОВЕК (Конфуций) → СМЪРТ (Конфуций).

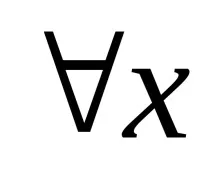
Понятието логическо следствие

НекаEе набор от формули (логика от първи ред), аCе отделна формула.

ФормулаCсе наричалогическо следствиеот набора от формулиE, ако е вярна при всички интерпретации, при коитовсички формулиот набораEса едновременно верни.

Използвайки това определение, фактът на логическата последица може да бъде установен чрез изброяване на всички възможни интерпретации. В логиката на предикатите обаче такъв подход е невъзможен, тъй като всяка формула има безкраен брой интерпретации (поради безкрайния набор от области на интерпретации).

Набор от формули се нарича неудовлетворим, ако няма интерпретация, при която всички формули от този набор са едновременно верни:

E╞C

– неосъществимо.

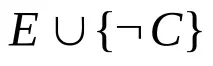
По този начин принципът на дедукцията свежда проблема за логическото следствие до проблема за невъзможността на набор от формули.

За да се докаже неприложимостта на набор от формули, се използва методът на разделяне.

АкоXиYса клаузи, тогава формулата

се наричарезолвент.

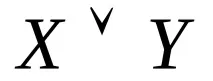
Правило за разрешаване: некаx,yса произволни формули иAе атом (елементарна формула), тогава:

→е правило за разрешаване.

,

, след това

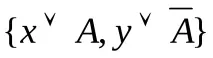
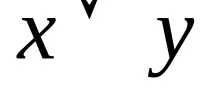
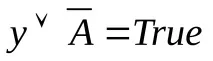
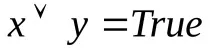
Да предположим, че

, след това. Така.

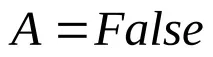
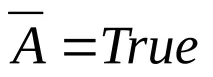
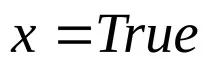
Разгледайте случая, когато x и y са дизюнкти (дизюнкция на атоми).

Всяка формула може да бъде преобразувана в нейния логически еквивалентен CNF (конюнктивна нормална форма).

Дизюнкт, съдържащ поне една буква, е удовлетворима формула (тоест е верен при определени интерпретации).

Единствената неудовлетворима клауза е празна клауза, т.е. клауза, която не съдържа нито един знак. Такива клаузи ще бъдат обозначени по-нататък с константата F (от False).

Алгоритъм за преобразуване на формули в CNF (по примера на пропозиционалната логика)

1). Елиминиране на връзки, импликации и еквивалентности:

2). Намаляване на обхвата на отрицанията, така че да се отнасят до елементарни формули:

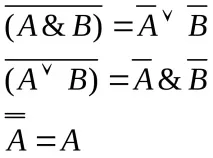
3). Закон за разпределение:

Твърдение 1:некаEе набор от формули,

са формулите на този набор и╞Zе логическо следствие.Тогава добавянето на формулатаZкъм набораEне променя неговата изпълнимост/невъзможност.

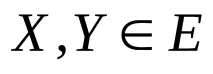
Твърдение 2:добавянето на разтворители към оригиналния набор не променя неговата удовлетворимост/неудовлетворимост.

За да конструираме резолвента, намираме клаузи, съдържащи контра-двойка (двойка, която има противоположни стойности) и конструираме резолвента.

–родителски клаузи,

е техният разтворител.

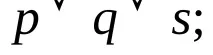
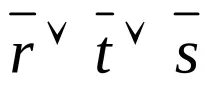
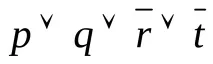
Пример 2: разгледайте 2 клаузи с един литерал

и, тяхната резолвента е празната клаузаF.

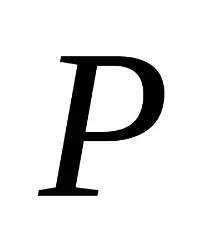
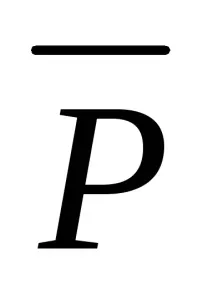
По този начин алгоритъмът на метода за разрешаване предполага последователно генериране на резолвенти от различни двойки родителски клаузи, докато се получи празна клауза. Това означава, че множеството е неудовлетворимо и по този начин логическото следствие е доказано.

Ако празната клауза не може да бъде получена, тогава наборът е удовлетворим и означава, че логическото следствие не се осъществява.

Теорема на Робинсън:ако наборът от клаузи е неудовлетворим, този факт винаги може да бъде установен с помощта на метода на разделяне в краен брой стъпки. Можем да кажем, че методът за разрешаване е пълен за даден проблем.

Общи предимства на логиката от първи ред

Логиката от първи ред има редица полезни свойства, които я правят много привлекателна като един от основните инструменти за формализиране на знания:

---