LAB_ECONOMETRIKA 1-2 - Страница 2
1. Постройте диаграма на корелационното поле.
2. За да характеризирате зависимостта на y от x, изчислете параметрите на линейната функция. Параметрите на регресионното уравнениеa,bсе определят по формулите:
След изчисленията трябва да се получи следното регресионно уравнение:y=38.81 +28.38*х
3. Тясността на линейната връзка и степента на вариация се оценяват с помощта на коефициента на корелация (r) и детерминацията (R 2 ). Коефициентът на детерминация показва какъв процент от вариацията Y се обяснява с поведението на фактора X.
Коефициент на корелация на линейна двойка:
Коефициент на определяне:
4. В корелационното поле начертайте регресионното уравнение. За това:
– според първоначалните данни се добавя линия на тренд чрез командатаДиаграма–Добавяне на линия на тренд;
– в командния прозорецTrendlineизберете типа на тенденцията „Линеен“ и в разделаПараметриактивирайте параметритепокажете уравнението на диаграмата,поставете стойността на надеждността на приближението R2на диаграмата
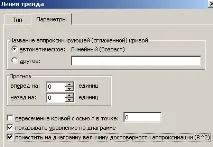
Фигура 3 - Прозорец "Линия на тенденция"
В резултат на това вземете графика на регресионното уравнение върху корелационното поле:
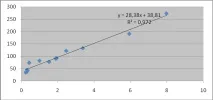
Фигура 4 - Поле на корелационна зависимост
5. Заместване на действителните стойностих,в регресионното уравнение за определяне на теоретичните стойности
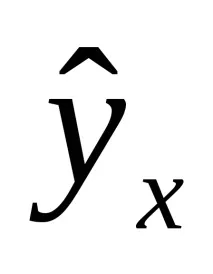
6. Качеството на модела се определя от средната апроксимационна грешка. Оценете модела чрез средната грешка на приближението Ā:
Средно изчислените стойности на ỹ за линейния модел се различават от действителните стойности на y с 12,51%.
Лабораторна работа №3. Оценка на значимостта на уравнението на линейната регресия и прогнозиране
Задача 1.Определете зависимостта на входа вефектът на жилищните сгради от инвестиции в жилищно строителство в регионите на република Казахстан. Оценете значението на регресионното уравнение и неговите параметри.
Таблица 5 - Данни за съставяне на уравнение на линейна регресия
Инвестиции, милиони тенге,x
1. Конструирайте линейно сдвоено регресионно уравнениеyотx,, което определя зависимостта на въвеждането в експлоатация на жилищни сгради от инвестициите в жилищно строителство.
2. На базата на първоначалните и изчислените стойности изградете корелационното поле и тренда на уравнението на линейната регресия.
3. Изчислете линейния коефициент на двойна корелация, коефициент на детерминация.
4. Оценка на адекватността на модела. Средна апроксимационна грешка и коефициент на еластичност.
5. Оценете статистическата значимост на регресионните и корелационните параметри.
6. Изпълнете прогноза за въвеждане в експлоатация на жилищаyс прогнозирана средна стойност на инвестициятаxс 20%.Оценете точността на прогнозата, като изчислите грешката на прогнозата и нейния доверителен интервал.
7. Добавете прогнозната стойност на резултантната характеристикаyкъм графиката на уравнението на линейната регресия.
8. Използвайки пакета за анализ на данни (Service–Data Analysis–Regression), получете параметрите на линейна регресия, корелации, доверителни интервали, т.е. показване на резултатите от регресионната статистика, дисперсионния анализ и заключението на остатъците.
1. Конструирайте регресионно уравнение на линейна двойкаизползвайки метода на най-малките квадрати.
Използване на формули за изчисление:
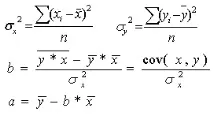
Заключение:С увеличаване на инвестициите в жилищното строителство с 1 милион тенге, въвеждането в експлоатация на жилища ще се увеличи леко със средно 0,055 кв.м.
На диаграмата на корелационното поле на зависимостта на променливите x, y, конструирайте поредица от точки, като използвате изчислените стойности


Фигура 5 - Тенденция на уравнението на линейната регресия y = 16,65 + 0,055 x
3. Изчислете коефициента на корелация на линейната двойка и коефициента на детерминация.
Изход:Директна положителна връзка. Коефициентът на детерминация показва, че 64% от вариацията във въвеждането в експлоатация на жилища (y) се обяснява с вариацията в инвестициите в строителство x.
4. Оценете качеството на регресионното уравнение като цяло, като използвате F-теста на Fisher. Ако F 2 е незначителен; ако F> Ftab, тогава R2 е значим.
Действителната стойност на F-критерия:
се сравнява с табличната стойност Ftabl=4,75 от таблицата F-тест на Fisher.
Заключение:Регресионното уравнение е значимо при ниво на значимост α = 0,05.
5. Оценката на адекватността на модела се определя от средната апроксимационна грешка:
Изчислете коефициента на еластичност:
Индексът на еластичност показва увеличение с 0,49% на вложените кв.м. жилища с ръст от 1% инвестициите в строителството.
6.Оценете статистическата значимост на регресионните параметри, като използватеt-Student's статистики.
Основната хипотеза е за статистически незначими показатели
Определете стандартните отклонения Sa, Sb на параметрите a и b от техните оценки:
Изчислете действителнитеt-статистики:
За броя на степените на свобода df=n-2=12 и α=0 ttable=2.178.
Ако tfact>ttable, тогава хипотезата Ho се отхвърля, т.е.a,bне са произволно различни от нула и са статистически значими.
Определете пределната грешка за всеки индикатор:
Изчислете доверителните интервали, като използвате следните формули:
В резултат на това вземете[5.3; 28,0] и b [0,03; 0,08]
Резултат:Анализът на горната и долната граница на доверителните интервали води дозаключението, че с вероятност p = 1- = 0.95, където =0.05, параметритеaиb,, намиращи се в посочените граници, не приемат нулеви стойности, т.е. не са статистически значими и са значително различни от нула.
7.Изпълнете прогнозата за въвеждане в експлоатация на жилищатаyс прогнозираната средна стойност на инвестициятахс 20%. Оценете точността на прогнозата, като изчислите грешката на прогнозата и нейния доверителен интервал.
Ако прогнозната стойност на инвестицията е: , тогава прогнозната стойност на въвеждане в експлоатация на жилищата ще бъде:
Стандартно отклонение (грешка) на прогнозата:
Пределната прогнозна грешка, която в 95% от случаите няма да бъде превишена, ще бъде:
Доверителен интервал на прогноза: [3,09; 68.51]
Добавете прогнозната стойност на резултантната характеристика y към графиката на уравнението на линейната регресия.
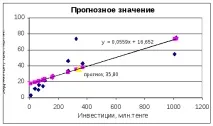
Фигура 6 - Прогнозна стойност въз основа на уравнението на линейната регресия
8. Показване на сумите за регресионна статистика, анализ на дисперсията и извеждане на остатъците с помощта на командатаУслуга–Анализ на данни–Регресия. Вземете параметри на линейна регресия, корелации, доверителни интервали и остатъци.
Задача 2.Според проучване на осем групи семейства са известни данни за връзката между разходите на домакинството за храна и семейния доход. Оценете значимостта на съставеното регресионно уравнение и неговите параметри.
Таблица 6 - Данни за съставяне на уравнение на линейна регресия