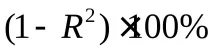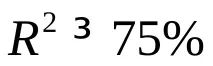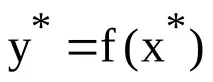Лабораторна работа 4 Тема Регресионен анализ

Регресионното уравнение на линейната двойка изглежда така:

Използвайки това уравнение, променливата Y се изразява чрез константата a0 и наклона на линията (или наклона) a1, умножен по стойността на променливата X. Константата a0 се нарича още пресечна точка, а наклонът е регресионен коефициент. Параметрите на уравнението могат да бъдат определени с помощта на метода на най-малките квадрати (LSM)

Най-малки квадрати

(в референтните системи на англоезични програми - метод на най-малките квадрати, LS) е един от основните методи за определяне на параметрите на регресионните уравнения, който дава най-добрите линейни безпристрастни оценки. Именно той се използва в MS Excel. Линеен - отнася се до естеството на връзката на променливите. Безпристрастен означава, че очакваните стойности на регресионните коефициенти трябва да бъдат истинските коефициенти. Тоест, точките, конструирани от оригиналните данни, трябва да лежат възможно най-близо до точките на регресионната линия. Същността на този метод е да се намерят параметрите на модела, при които сумата от квадратите на отклоненията на емпиричните (действителните) стойности на получената характеристика от теоретичните, получени от избраното регресионно уравнение, т.е.

,

където

е стойността, изчислена съгласно уравнението на регресия;–отклонение(грешка, остатък) (фиг.1);n е ​​броят на двойките начални данни.

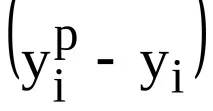
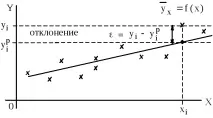
Ориз. 1 Концепцията за отклонение

за случая на линейна регресия

При регресионния анализ се приема, че математическото очакване на случайната променлива

е равно на нула и нейната дисперсия е еднаква за всички наблюдавани стойности на Y. От това следва, че разсейването на данните в близост до регресионната линия трябва да бъде същото завсички стойности на параметъра X. В случая, показан на фиг. 2, данните са неравномерно разпределени по линията на регресия, така че методът на най-малките квадрати не е приложим в този случай.

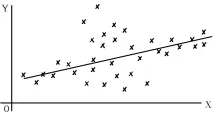
Фиг.2. Неравномерно разпределение на базовите точки по линията на регресия

След като извършим необходимите трансформации, получаваме система от две уравнения с две неизвестни a0 и a1, които ще намерим чрез решаване на системата.

(1)

(2)

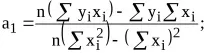
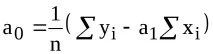
Посоката на връзката между променливите се определя въз основа на знаците (отрицателни или положителни) на регресионния коефициент (коефициент a1).

Ако знакът на регресионния коефициент е положителен, връзката между зависимата променлива и независимата променлива ще бъде положителна. В нашия случай знакът на регресионния коефициент е положителен, следователно връзката също е положителна.

Ако знакът на регресионния коефициент е отрицателен, връзката между зависимата променлива и независимата променлива е отрицателна (обратна).

За да се анализира общото качество на регресионното уравнение, обикновеномножествен коефициент на детерминацияR2, наричан още квадрат на множествения корелационен коефициент R. R 2 (мярка за сигурност) винаги е в рамките на интервала [0;1].

Ако стойността на R 2 е близка до единица, това означава, че изграденият модел обяснява почти цялата променливост на съответните променливи. Обратно, стойност на R-квадрат, близка до нула, показва лошо качество на конструирания модел.

Коефициентът на определяне R 2 показва колко процента (

) намерената регресионна функция описва връзката между първоначалните стойности на факторите X и Y

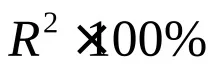
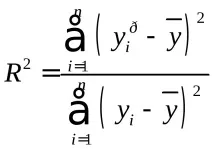
където

е обяснената вариация;- обща вариация (фиг. 3).

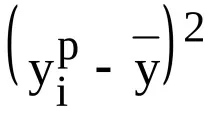
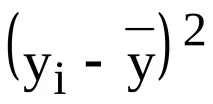
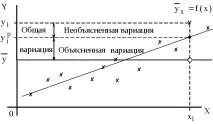
Ориз. 3 Графична интерпретация на коефопределения за случая на линейна регресия

Съответно, стойността

показва колко процента от вариацията на параметъра Y се дължи на фактори, които не са включени в регресионния модел. При висока () стойност на коефициента на определяне е възможно да се направи прогнозаза конкретна стойност.

---