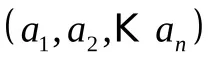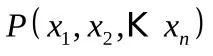Лекция 2 Отношение
Изследователят винаги се интересува от различни свойства на обектите: свойства, свързани с отделни обекти (например "да бъде жена", "да бъде бял", "да има ниска топлопроводимост") и свойства, които характеризират връзките между няколко обекта (например свойствата "да бъдат роднини" и "да бъдат повече" се отнасят за двойки обекти, свойството "да бъде между" - за тройки обекти, свойството "да се намират във върховете на квадрат" - за четири обекта).
Такива свойства се наричат отношения. В този случай свойствата на отделните обекти се наричат унарни (едноместни) релации, свойствата, свързани с двойки обекти -бинарни релации, свойствата, свързани с набори отnобекти, -n-арни релации
Понятието релация е много важно не само от математическа гледна точка. Концепцията за връзка всъщност е в основата на цялата теория на базите данни. Релациите са математически еквивалент натаблици.
ДефиницияВръзкие един от начините за указване на връзки между елементи на набор.
Примерза отношения от училищен курс по математика са:
върху множеството от цели Z, отношенията "разделяне", "разделяне", "равно", "по-голямо от", "по-малко от", "взаимопрости";
върху множеството от прави в пространството отношенията са "успоредни", "взаимно перпендикулярни", "пресичат се", "пресичат се", "съвпадат";
на набор от кръгове "пресичат", "докосват".
Фактът, че кортеж (x,y) принадлежи към релацияR, често се означава синфикснотация:xRy.
Примери за такива записи от курс по математика са:x>y,a=b,ml.
Методи за установяване на връзки
Отношенията могат да бъдат зададени:
формулиy = x2+5x - 6- двоични отношения върху множеството от реални числа;
формулаx+y= любов-бинарна връзка на набор от хора.
ДефиницияМатрица на двоична релация–е матрица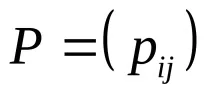
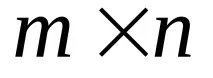
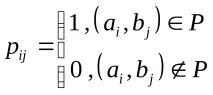
или1 –ако има връзка
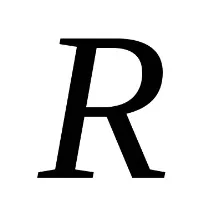
задайте съотношението "да бъде строго по-малко от"

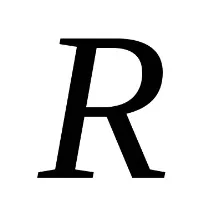
графично представянеВ това представяне елементите на множествотоXса представени чрез върхове на графика (точки от равнината), а елементите (x,y) на релациятаса представени чрез дъги (стрелки), свързващи първия компонентxна релацията с втория компонентy.
Декартово произведение на множества
В математиката доста често трябва да се работи не само с отделни елементи на набор, но и с подредени двойки от негови елементи. Използвайки две числа 3 и 5, можете да напишете 4 числа, важен е редът на числата или подреден набор.
ДефиницияLet-sets. Израз на формата където и се наричаподредена двойка.Като цяло може да се разглеждаподреден n-кортежот елементи илинабориликортеж.
Дефиниция.Два кортежа са равни, т.е. (a1. an) = (b1. bn) тогава и само ако за всяко i равенството ai= bi е в сила.
ДефиницияДекартово (директно) произведение на множествае набор от кортежи от вида
Декартовото произведениена тези множества е множеството от всички възможниn‑локални елементарни кортежи, които имат елемент от множеството


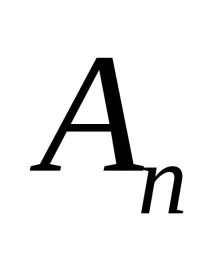
Тук множеството съдържадвойкиелементи, които, за разлика от множествата, имат строго определен ред (т.е. не могат да се разменят). За да се разграничат (подредените) двойки от множествата, те не са затворени във къдрави скоби, а в обикновени скоби.
ЗабележкаXY
ДефиницияСтепента на декартово произведениее броятnот наборите, включени в това декартово произведение.
Забележка.Ако всички набори са еднакви, тогава използвайте нотацията
Забележететермина „dкартезианска работа“Какво общо има великият френски математик и философ Рене Декарт? Той изобретил координати, които се наричат декартови. Множеството от точки в равнината може да се разглежда като пряко произведение на координатните оси.
ДефиницияНабор от елементарни кортежи с едно и също измерениеnсе наричамногоилиn-локалнарелация.
ПримерВръзката "по-малко от" за набор от цели числа може да бъде представена като набор от двойки числа
Теорема Kброят на всички елементи (т.е. елементарни кортежи) на декартово произведение ще бъде равен на произведението на мощностите на всички набори, използвани в това произведение, т.е.
ЗадачаТри пътя водят от град A до град B, а 4 пътя водят от град B до град C. По колко начина можете да стигнете от A до C през B?
Задачата първоначално е формулирана не като математическа задача, а като задача от реалния живот и следователно трябва да бъде преработена в математическа задача. В този случай е необходимо да се отделят съществените фактори от несъществените.
Наистина, ако в броенето на начините щевземете предвид времето от деня, скоростта и начина на придвижване (пеша, с кола, велосипед и т.н.), тогава задачата става изключително проста, когато се вземат предвид тези фактори, отговорът на задачата е: "Има безкрайно много начини."
Ако се абстрахираме от всички тези фактори и разберем пътя за стигане от A до C през B като подредена двойка (пътят, по който се движим от A до B; пътят, по който се движим от B към C), тогава решението на проблема може да се получи с помощта на концепцията за декартов продукт. Означават:
AB е множеството от пътища, водещи от A до B;
BC е набор от пътища, водещи от B до C.
Тогава математическата задача, до която е сведена първоначалната задача, изглежда така: "Намерете броя на елементите в декартовото произведение AB × BC."
AB×BC = AB BC = 3 4 = 12.
Отговор: 12 начина.
ЗабележкаВсяко множество може да се разглежда като декартово произведение от степен 1, тогава всяко подмножество, като всяко множество, може да се счита за релация от степен 1.
ЗабележкаНетривиалността на концепцията за връзка се проявява, когато степента на връзката е по-голяма от 1.
Тук има два ключови момента:
Всички елементи на релацията сакортежи от един и същи тип.
релация, се състои от три кортежа
Набор, състоящ се отразличничислови кортежи. Това множество не е релация нито в
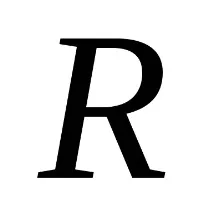
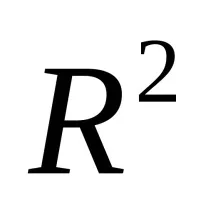

2. Връзката включване всички възможни кортежиот декартовия продукт. Това означава, че за всяка релация имакритерий, който ви позволява да определите кои кортежи са включени в релацията и кои не.
ДефиницияКортеж