Лекция № 3 Методи за описание на свойствата на елементите на автоматизацията
Въпроси, разгледани в лекцията:
Математически характеристики на елементите за автоматизация. Диференциални уравнения, предавателни функции, честотни характеристики. Понятия за типични връзки на системи за управление и техните характеристики. Типични свързващи връзки.
Системите за управление са набор от елементи, в които протичат процеси от различно физическо естество. Системата може едновременно да съдържа механични, електрически, пневматични и други елементи, взаимодействащи помежду си според съответните закони, като същевременно преобразуват един вид енергия в друг.
За изчисляване и изследване на системи за автоматично управление елементите на системата трябва да бъдат представени чрез универсални математически характеристики.
Те включват диференциални уравнения, трансферни функции, преходни функции (криви на ускорение), честотни характеристики.
Диференциални уравнения.За елемент (система) с едно входно действиеx(t)и една изходна стойностy(t), линейно диференциално уравнение, описващо неговите свойства, обикновено се представя като:
(3.1)
Изразът (3.1) се нарича уравнение на динамиката или уравнение на движението на елемент във времето. Параметрите на уравнението(aiи bi)зависят от конструкцията на елементите, масите на движещите се части, обемите, капацитета и т.н.
Ако в уравнение (3.1) всички производни се приравнят на нула, тогава получаваме статичната характеристика на елемента (системата):
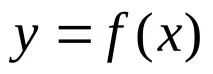
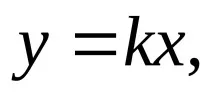
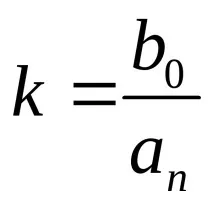
Изчисляването на системите за управление е значително опростено, ако не използватедиференциални уравнения на елементите на системата и техните предавателни функции.
Трансферна функцияе отношението на изходната стойност на връзката към входната стойност при нулеви начални условия. В този случай тези количества се изразяват в операторна форма, т.е.
, (3.3)
Всяка временна функцияy(t),x(t)може да се трансформира в нейния образY(p)иX(p)в пространството на Лаплас, където всички функции зависят не отt, а от променливатаp. В пространството на Лаплас диференцирането във времето, например, на областтаdy(t)/dtсъответства на умножение по променливатаpв пространството на Лаплас –pY(p).По същия начин,d2y(t)/dt2=p2Y( p).B В по-нататъшни математически трансформации операторът"p"се разглежда като алгебричен фактор, който може да бъде поставен в скоби, намален и т.н.
Преходна функция. Математическото решение на уравнение (3.1) описва поведението на изходната стойност y(t) за даден закон на промяна на входната стойностx(t)и дадени начални условия. Сред многото решения стъпаловидно преходната функция иликривата на ускорениетое от голямо практическо значение - това е реакцията на изходната стойност на елемента към стъпаловидно изменение на входаx=1(t-t0)при нулеви начални условия (фиг. 3.1). Кривата на ускорението често се взема експериментално върху работния контролен обект. Обработката на кривата на ускорението ви позволява да оцените статичните и динамичните свойства на обекта на регулиране, за да получите трансферна функция.
Честотна характеристика. Важна характеристика на динамичните свойства на даден елемент (система) е неговата реакция на хармонични синусоидални влияния. Честотни характеристикиполучено чрез заместване на променливата"p"в пространството на Лаплас с въображаемата честотаjw,тукj=
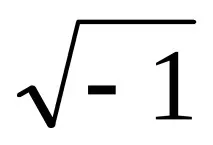

Типични връзки на системи за управление
Въпреки голямото разнообразие от елементи за автоматизация, могат да се разграничат само няколко типични (елементарни) връзки, с помощта на които ще бъде възможно да се изградят всякакви по-сложни връзки, срещани в практиката.
Типичните връзки се разделят на пропорционални (усилващи), апериодични (инерционни), осцилаторни, интегриращи, диференциращи и транспортно забавящи връзки.
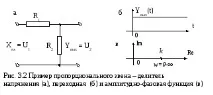
Пропорционална схема.Примери могат да бъдат делител на напрежение, лост, механична скоростна кутия, усилващо стъпало и т.н. За тези връзки е валидна пропорционална връзка между входната и изходната стойност:
, (3.4)
къдетоkе коефициентът на предаване (усилване).
Трансферната функция на тази връзка е числено равна на коефициента на трансфер:
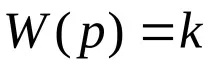
Пример за пропорционална връзка и нейните характеристики е показан на фиг. 3.2.
Апериодична връзка от първи ред(фиг. 3.3). Апериодичната връзка се описва с диференциалното уравнение:
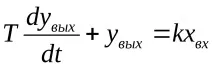
къдетоТ- времева константа;
k- коефициент на предаване.
Трансферната функция на тази връзка се определя от израза:
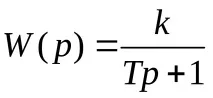
Примери за апериодична връзка са топлинен обект, където входът е например разход на гориво, а изходната стойност е температура. Друг пример е технологичен резервоар със свободен поток от течност, тук входният сигнал е дебитът на входящата течност, изходният сигнал е нейното ниво в резервоара.
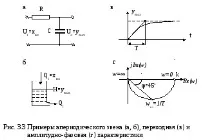
Мярката за инерция на връзката евремеконстантаT.
Амплитудно-фазовата характеристика на връзката се представя с израза:
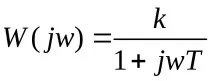
Вибрационна връзка.Осцилаторната връзка се описва от уравнение от втори ред:
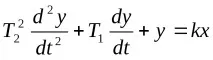
k– коефициент на предаване.
От (3.9) следва трансферната функция на връзката:
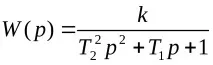
На фиг. 3.4 показва примери за физическо изпълнение на осцилаторна връзка: а - колебателна верига с R, L, C параметри и механична система, включваща пружина и хидравличен демпфер (b).
Преходната функция (решение на уравнение 3.9) може да има апериодична (пунктирана линия на фиг. 3.4c) и осцилаторна форма (плътна линия).

Амплитудно-фазовият честотен спектър на осцилаторната връзка (фиг. 3.4 d) се различава по това, че неговият ходограф улавя отрицателната област на реалната ос на координатното пространство.
Интегрираща връзка.Уравнението на връзката в интегрална форма изглежда така:
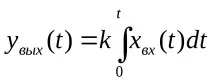
или в диференциална форма
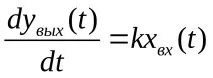
Преминавайки към формата на оператора, получаваме трансферната функция:
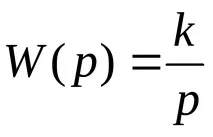
Горните уравнения са валидни заидеалнияинтегратор.
Има известна инерция в реалната интегрираща връзка, така че диференциалното уравнение и трансферната функция на реалната интегрираща връзка имат формата:
и
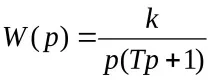
Всяка технологична колекция от материали може да служи като пример за реална интегрираща връзка, където входният сигнал е потокът от материал, а масата му в колекцията може да се приеме като изходна стойност.
На фиг. 3.5 показва основните характеристики на интегриращата връзка.

Диференциатор. Изходната стойност на тази връзкапропорционално на скоростта на промяна на входа:
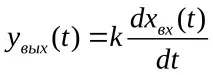
откъдето трансферната функция има формата:
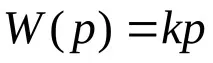
В общия случай уравнението на реална диференцираща връзка:
, (3.13)
откъдето предавателна функция:
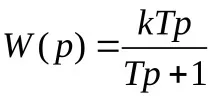

Връзка на транспортно (чисто) забавяне.За разлика от предишните връзки, тази връзка се описва от уравнение със забавен аргумент:
, (3.14)
къдетоτе времето на забавяне при транспортиране.
Трансферната функция и AFC на връзката имат формата:
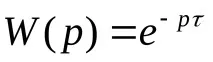
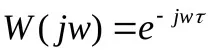
Графично амплитудно-фазовата характеристика е представена като кръг с единичен радиус с център в началото.
Наличието на връзка за забавяне на транспорта в системата за управление значително намалява качеството на управление и понякога прави системата за управление нестабилна, което ще бъде обсъдено по-долу.
Динамични характеристики на типичните връзки на връзките.
В системите за управление връзките могат да бъдат свързани в различни комбинации. Има три основни типа свързване на връзки, комбинирайки които, можете да стигнете до всяка сложна система. Такива връзки включват: последователни, паралелни и антипаралелни (покритие на връзката за обратна връзка) връзки.
Структурни диаграми на различни връзки на връзките са показани на фиг. 3.8.
В случай на свързване на две връзки, имаме общи трансферни функции за случаите "a" и "b" имат формата:
И
Връзката обратно към гърба (фиг. 3.8 c) често се нарича връзка с покритие на връзката за обратна връзка.
В този случай трансферната функция на общата връзка е представена с израза:
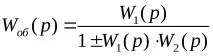
В същото време знакът "+" се поставя в знаменателя, ако обратната връзка е отрицателна и"-" за положителна обратна връзка.
За да се гарантира стабилността на елементите на автоматизацията и системите като цяло, се използват предимно отрицателни обратни връзки.
Избройте начините за представяне на динамичните характеристики на ACP елементи.
Дайте общо диференциално линейно уравнение за всеки елемент от ASR.
Обяснете концепцията за трансферна функция на ASR елемент, как да получите трансферна функция въз основа на диференциално уравнение.
Обяснете концепцията за преходната функция на елемент за автоматизация.
Опишете честотните характеристики на ASR елементите.
Избройте типичните връзки на регулаторните системи.
Характеристики на пропорционалната връзка.
Дайте примери за апериодична връзка от първи ред и нейните характеристики.
Представете всички динамични характеристики на реална и идеална диференцираща връзка.
Дайте характеристиките на осцилиращата връзка.
Как се определя коефициентът на затихване на осцилаторна връзка?
Представете динамичните характеристики на реална и идеална интегрираща връзка.
Литература за тема номер 3: [1], [2], [6]